Enseignement scientifique de première – Partie 1 – Une longue histoire de la matière – Des édifices ordonnés : les cristaux
- Le chlorure de sodium
- Solides cristallins et solides amorphes
- La maille
- Population d’une maille
- Paramètre de maille
- Volume d’une maille
- Masse volumique d’une maille
- Compacité d’une maille
- Maille cubique simple
- Maille cubique faces centrées
- Cristaux, minéraux et roches
Le chlorure de sodium
Le chlorure de sodium (utilisé comme sel de cuisine ou pour le déneigement des routes) un exemple de solide cristallin.
Il est présent naturellement dans certaines roche, il peut être obtenu par évaporation de l’eau mer (cette technique est exploitée dans les marais salants).
Il s’agit d’un solide ionique de formule chimique NaCl :
- il est constitué d’ions sodium Na+
- il est constitué d’ions chlorure Cl–
- Ces ions sont en proportions identiques (il y a autant d’ions chlorure que d’ions sodium)
La cohésion du chlorure de sodium est assurée par les forces de Coulomb attractives qui s’exercent entre les ions positifs (sodium) et les ions négatifs (chlorure) .
( voir cours de première spécialité sur la cohésion des solides ioniques )
Pour que les forces de Coulombs puissent assurer la cohésion de ce solide ionique, les forces attractives (entre cations et anions) doivent être plus intenses que les forces répulsives (entre ions de même signe) : il en résulte une alternance d’ions sodium et d’ions chlorure.
Ces ions forment une structure élémentaire de base cubique où les ions sont répartis.
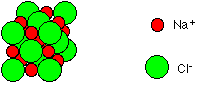
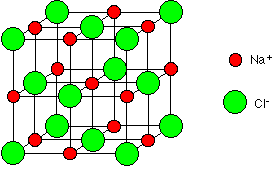
Cette structure se répète dans toute les directions de l’espace pour former un réseau cristallin.
On retrouve cette forme cubique à l’échelle macroscopique lorsqu’on observe des cristaux de chlorure de sodium.
Le chlorure de sodium est composé d’un empilement régulier d’ions chlorure et d’ions sodium formant des structures se répétant de manière régulière.
Solides cristallins et solides amorphes
Un solide cristallin est un milieu ordonné comportant une structure microscopique élémentaire qui se répète dans les trois directions de l’espace.
Le graphite, le diamant, le quartz, la glace, sont des exemples de solides cristallins.
La répétition de cette structure microscopique élémentaire constitue des cristaux dont la géométrie reflète celle de cette structure (La répétition d’une structure microscopique cubique se traduit par exemple par des cristaux de forme cubique)
Les solides cristallins ne peuvent se former que lors de processus suffisamment lents (solidification, précipitation) qui permettent aux entités microscopiques s’orienter et d’adopter les configurations les plus stables.
Lorsqu’un liquide se refroidit de manière brutale les entités microscopiques n’ont pas la possibilité de s’organiser et forment un solide dit amorphe où les structures élémentaires ne sont pas ordonnées.
Un solide est dit amorphe si ses structures élémentaires ne se répètent de manière régulière : c’est un milieu désordonnée.
Le verre, l’obsidienne sont des exemples de milieux amorphes.
Cet agencement désordonné qui caractérise les solides amorphes au niveau microscopique a une influence sur leurs propriétés macroscopiques. En particulier les solides amorphes se brisent plus facilement que les solides cristallins.
Le refroidissement lent d’un liquide permet de former un solide cristallin alors qu’un refroidissement rapide conduit à la formation solide amorphe.
La précipitation lente d’ions en solution (par évaporation progressive du solvant par exemple) permet de former des cristaux alors qu’une précipitation rapide (avec chauffage de la solution) conduit à la formation d’un solide amorphe.
En général la formation lente d’un solide conduit à milieu cristallin alors qu’une formation rapide conduit à un milieu amorphe
La maille
Une maille est la structure géométrique qui se répète de manière périodique dans différentes directions de l’espace pour former un cristal.
La plus petite maille constituant un cristal (celle qui ne peut pas être divisée en mailles plus petites) est appelée maille élémentaire.
Une maille est caractérisée :
- par sa forme géométrique (cubique, hexagonale)
- par la répartition des entités chimiques
- par ses dimensions (qui dépend de la taille des entités chimiques qu’elle héberge)
- par son volume (lié à ses dimensions)
- par sa masse (qui dépend de celle des entités chimiques)
- par sa multiplicité ou population (nombre d’entités chimiques qu’elle comporte)
- sa compacité
Population d’une maille
Définition
La population d’une maille, aussi appelée « multiplicité », souvent notée « N » correspond au nombre d’atomes appartenant réellement à une maille.
Elle ne tient compte que des atomes ou des « portions d’atome » inclus dans la maille.
Si un atome est partagé entre deux mailles alors chaque maille ne « possède » que la moitié ( un demi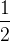 
) de cet atome : c’est le cas d’un atome situé au centre d’une face de maille cubique.
Si un atome est partagé entre quatre mailles alors chaque maille ne comporte qu’un quart (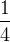
) de cet atome : c’est le cas d’un atome situé sur l’arrête d’une maille cubique.
Si un atome est partagé entre 8 mailles alors chaque maille ne contient qu’un huitième (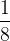
) de cet atome : c’est le cas d’un atome situé au sommet d’une maille cubique.
Une maille cubique simple comporte 8 atomes sur 8 sommets : 8 x 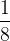=1 soit une population N = 1
Une maille cubique simple renferme l’équivalent d’un atome.
Une maille cubique faces centrées comporte
Soit une population totale N = 3 + 1 = 4
Une maille cubique face centrée renferme l’équivalent de 4 atomes.
Paramètre de maille
Définition
Un paramètre de maille correspond à la longueur d’un coté de la maille.
Si la maille est cubique alors il n’y a qu’un seul paramètre de maille (puisque tous les cotés d’un cube ont même longueur!), il est noté « a »
Dans le cas d’un corps simple c’est à dire d’un minéral constitué d’une seule sorte d’atome il est possible d’établir une relation entre le paramètre de maille et le rayon atomique ratome.
Dans le cas d’un d’une maille cubique simple les deux atomes situés aux sommets d’une même arrêtes sont en contact.
On pourrait schématiser une face de cette manière :
Par conséquent on a l’égalité suivante :
soit a = 2ratome ou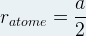 
pour une maille cubique simple
Dans le cas d’une maille cubique face centrée le contact se fait entre les atomes de la diagonale d’une face.
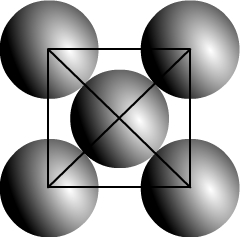
Cette diagonale a pour longueur ratome + 2ratome + ratome = 4 ratome
La longueur de cette diagonale peut aussi être exprimée grâce au théorème de Pythagore dans le triangle rectangle isocèle :
diagonale2 = a2 + a2
diagonale2 = 2a2
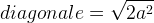
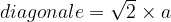
D’où l’égalité :
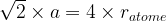
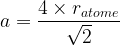
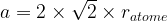
Dans une maille cubique face centrée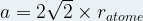 
et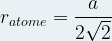 
Volume d’une maille
Le volume d’un cube se calcule grâce à la formule
V = coté x coté x coté donc
Vmaille = a3
Dans le cas d’une maille cubique simple a = 2 x ratome donc
Vmaille cubique simple = (2ratome)3
Vmaille cubique simple = 23 x (ratome)3
Vmaille cubique simple = 8 (ratome)3
Dans le cas d’une maille cubique faces centrées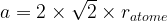 
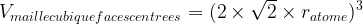
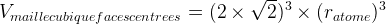
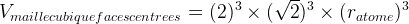
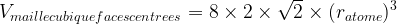
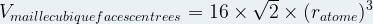
Masse volumique d’une maille
La masse volumique d’une maille correspond aussi à celle du cristallin
ρmaille = ρcristal
La masse volumique est définie comme le rapport de masse de matière divisée par le volume occupé par cette matière :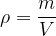 
à l’échelle d’une maille le volume V est celui de la maille et la masse est celle des atomes des cette maille.
Si la maille comporte une population de « N » atomes de masse matome alors la masse a pour valeur m = N x matome
La masse volumique d’une maille a donc pour valeur :
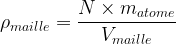
Remarque : la masse d’un atome peut être déterminée à partie de la masse molaire atomique indiquée dans le tableau périodique :
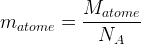
où NA correspond au nombre d’Avogadro (NA = 6,02.1023)
- Dans le cas d’une maille cubique simple
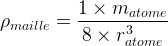
- Dans le cas d’une maille cubique faces centrées
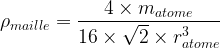
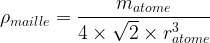
Compacité d’une maille
Définition
La compacité indique la proportion d’espace occupé par la matière dans une maille
Elle se note « c » et n’a pas d’unité.
On peut l’exprimer à l’aide de la relation suivante :
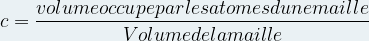
Etant donné qu’un atome est modélisé par une sphère de rayon ratome son volume est
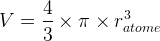
L’expression de la compacité devient donc :
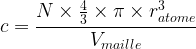
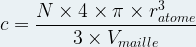
- Pour une maille cubique simple
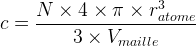
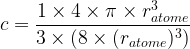
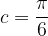
c = 0,52
Cela signifie que 52 % de l’espace de la maille cubique simple est occupée par de la matière tandis que le reste (48 %) est vide.
- Pour une maille cubique faces centrées
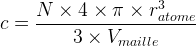
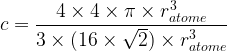
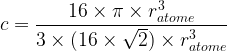
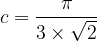
c = 0,74
Cela signifie que 74% de l’espace de la maille cubique faces centrées est occupée par de la matière , il s’agit de la compacité maximale possible.
La maille cubique simple
La maille cubique simple (parfois notée CS) est une maille de géométrique cubique :
La longueur du coté est appelée paramètre de maille et souvent noté « a »
Dans le cas où les entités chimiques sont des atomes tous identiques (c’est par exemple le cas dans un métal) alors à chaque sommet de la maille se trouve le centre d’un atome.
Puisqu’un cube possède 8 sommets il en résulte que 8 atomes sont répartis aux sommets d’une maille.
Attention, cela ne signifie pas qu’une maille comporte 8 atomes « complets » car chaque maille est accolée à d’autres mailles sur le même plan, sur le plan inférieur et sur le plan supérieur.
Représentation d’une maille cubique simple
Dans un premier temps on représente un cube en perspective cavalière
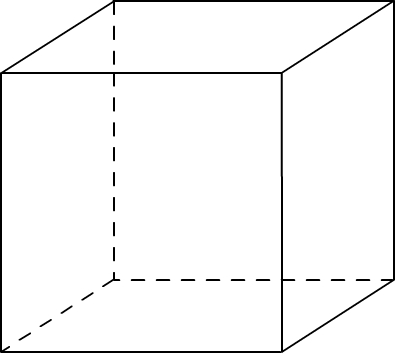
Si l’on souhaite une représentation éclatée il suffit de placer une petite sphère à chaque sommet du cube
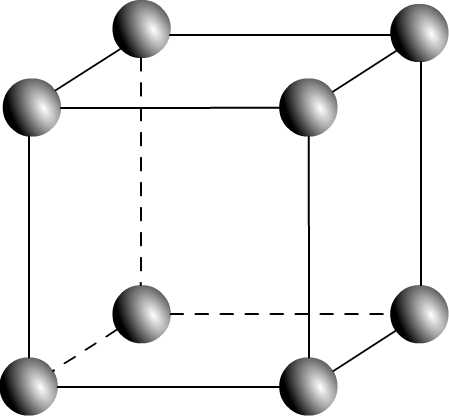
Cette une représentation qui permet de facilement visualiser la répartition des atomes dans l’espace mais qui n’est pas fidèle à la réalité.
En effet les structure cristallines sont compactes, les atomes sont au contact les uns avec les autres.
Si l’on représentait une face de la maille en respectant le critère de compacité on obtiendrait plutôt :
Exemples de cristaux à maille cubique simple : le polonium, la pyrite.
Caractéristique de ma maille cubique simple :
- Population : 1 atome par maille
- Paramètre de maille : a = 2ratome
- Volume de la maille : Vmaille cubique simple = 8 (ratome)3
- masse volumique de la maille :
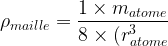ρmaille = 1 x matome / 8 (ratome)3 - Compacité : c = 0,52
Maille cubique faces centrées
On la note souvent CFC
Une maille cubique faces centrée est de géométrie cubique, elle dispose d’un atome à chaque sommet mais aussi d’un atome au centre de chacune de ses six faces (ce qui justifie le choix de ce nom !)
Représentation d’une maille cubique faces centrées en perspective cavalière
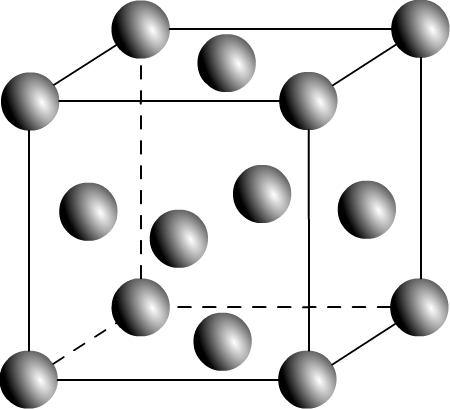
Si l’on respecte le caractère compact d’un cristal voici la représentation d’une face
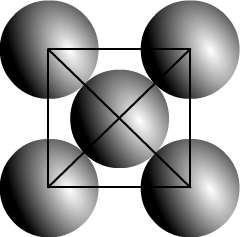
Il y a contact entre les atomes alignés sur la diagonale d’une face.
Exemples de cristaux à maille cubique faces centrées : l’aluminium, le tungstène, le cuivre.
Caractéristique de ma maille cubique faces centrées:
- Population : 4 atomes par maille
- Paramètre de maille :
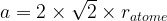
- Volume de la maille :
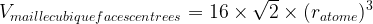
- masse volumique de la maille :
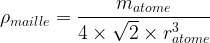
- Compacité : c = 0,74
Cristaux, minéraux et roches
Définition
Un cristal est définit par son type de maille et la nature des entités chimiques qui le constituent.
Par exemple un cristal de chlorure de sodium est caractérisé par une maille de type cubique faces centrées dont les entités chimiques sont des ions chlorure et des ions sodium.
Définition
Un minéral est une substance solide constituée d’un assemblage de cristaux identiques. Il est donc caractérisé par sa composition chimique et le type de maille de ses cristaux.
Par exemple le sel de cuisine, le diamant sont des minéraux.
Définition
Une roche est solide constituée d’un assemblage d’un ou plusieurs types de cristaux.
Par exemple le granit est une roche constituée, entre autres, de quartz et de micas
- Pour revoir ce cours
“Des édifices ordonnés: les cristaux” sous forme vidéo
- Pour s’exercer
Correction d’un exercice provenant d’un sujet d’examen ” Diamant et kimberlite“