Cours de physique-chimie | première spécialité
Ce cours correspond à la partie “2. La lumière : images et couleurs, modèles ondulatoire et particulaire – B) Modèles ondulatoire et particulaire de la lumière” du programme de première spécialité.
Il est situé dans la partie du programme “Ondes et signaux”
- La lumière est une onde électromagnétique
- Relation entre période, fréquence et longueur d’onde d’une onde électromagnétique
- Les différentes catégories d’ondes électromagnétiques
- La lumière est composée de photons
- Energie d’un photon
- Niveaux d’énergie d’un atome
- Diagramme d’énergie d’un atome
- Emission et absorption d’un photon par un atome
REVISER – AUTRES COURS DE PREMIERE SPECIALITE – APPROFONDIR ET DECOUVRIR
En guise d’introduction on peut d’abord lire “Les ondes électromagnétiques“
La lumière est une onde électromagnétique
La lumière est une onde périodique progressive de nature « électromagnétique» : elle correspond à la propagation de champs électriques et magnétiques oscillants.
Contrairement aux ondes mécaniques la lumière ne nécessite pas un milieu matériel pour se propager :
La lumière peut se propager dans le vide et aussi dans certains milieux matériels.
Comme toute autre onde périodique progressive une onde électromagnétique se caractérise par les grandeurs suivantes :
- Sa période « T » en seconde (s) (correspond à la durée d’une oscillation des champs électriques et magnétiques)
- Sa fréquence « ν » en Hertz (Hz) (correspond au nombre d’oscillations par seconde)
- Sa longueur d’onde « λ » en mètre (m) (correspond à la distance sur laquelle se propage l’onde pendant une période)
Dans le vide toutes les ondes électromagnétiques se propagent à une célérité :
c = 3,00.108 m.s-1
c= 3,00.105 km.s-1
Relation entre période, fréquence et longueur d’onde d’une onde électromagnétique
- Expression de la longueur d’onde λ :
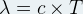
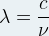
- Expression de la fréquence ν:
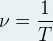
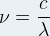
- Expression de la période T :
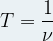
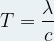
Les différentes catégories d’ondes électromagnétiques
On distingue différentes sortes d’onde électromagnétiques (par ordre de longueur d’onde croissante) :
- Les rayons ϓ (gamma) – longueur d’onde inférieure à 10 picomètres ( λ < 10-11 m)
- Les rayons X – longueur d’onde comprise entre 10 picomètres et 10 nanomètres (10-11 m < λ < 10-8 m)
- Les ultraviolets (UV) – longueur d’onde comprise entre 10 nanomètres et 400 nanomètres (10-8 < λ < 4.10-7 m)
- La lumière visible – longueur d’onde comprise entre 400 nanomètres et 800 nanomètres (4.10-7 m< λ < 8.10-7 m)
- Les infrarouges – longueur d’onde comprise entre 800 nanomètres et un millimètre (8.10-7 m< λ < 10-3 m)
- Les micro-ondes – longueur d’onde comprise entre 1 mm et 30 cm (10-3 m < λ < 3,0.10-1 m)
- Les ondes radios – longueur d’onde supérieure à 30 cm ( λ > 3,0.10-1 m)
Source : https://www.esa.int/Science_Exploration/Space_Science/Integral/The_electromagnetic_spectrum
Remarque
Il n’y a pas de frontière nette entre les différents domaines et il n’est pas rare de trouver de valeurs différentes en consultant plusieurs sources.
La lumière est composée de photons
Le modèle ondulatoire (qui modélise la lumière comme une onde) ne parvient pas expliquer toutes le propriétés de la lumière, dans certaines circonstances cette dernière se comporte comme si elle était constituée de particules distinctes.
Pour décrire certains aspects de la lumière il est parfois nécessaire de la modéliser non plus comme une onde mais comme un ensemble de particules : on peut décrire la lumière par un modèle dit particulaire.
D’après le modèle particulaire :
La lumière est composée d’un flux de particules appelées « photons »
Les photons sont des particule dites élémentaires (qui ne sont pas composées de particules plus petites) qui :
- ont une masse nulle (mphoton = 0 kg)
- ont une une charge électrique nulle ( qphoton = 0 C)
- ont chacun une énergie « E » appelée « quantum d’énergie » qui dépend de la longueur d’onde la lumière
- se déplacent dans le vide à une vitesse correspondant à la célérité de la lumière dans le vide ( dans le vide vphoton = 3,00.108 m.s-1)
Energie d’un photon
L’énergie d’un photon, aussi qualifiée de « quantum d’énergie », peut être calculée grâce à la relation de Planck-Einstein (souvent appelée seulement relation de Planck)
Relation de Planck – Einstein :
E = h x ν
où :
- h est la constante de Planck (h = 6,63 .10-34J .s)
- ν est la fréquence de la lumière ( en Hertz)
- E est l’énergie du photon (en Joule)
D’après cette relation l’énergie d’un photon est proportionnelle à la fréquence de la lumière.
Si l’on connaît la longueur d’onde (λ) d’un rayonnement alors on peut en déduire la valeur de la fréquence grâce à la relation suivante:
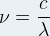
Si l’on remplace la fréquence qui intervient dans la relation de Planck par cette expression alors on obtient une relation qui permet de calculer directement l’énergie d’un photon à partir de la longueur d’onde la lumière :
E = h x ν
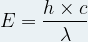
Avec :
- E, l’énergie du photon (J)
- h, la constante de Planck (h = 6,63 .10-34J .s)
- λ, la longueur d’onde (m)
L’énergie d’un photon est souvent exprimée en électronvolt
C’est une une unité de symbole eV avec l’équivalence :
1eV = 1,6.10-19 J
Pour convertir des joules en électronvolts on divise par 1,6.10-19
Pour convertir des électronvolts en Joules on multiplie par 1,6.10-19
Voir aussi cours sur l’électronvolt
Niveaux d’énergie d’un atome
Un atome est caractérisé par l’énergie qu’il possède du fait de la répartition de ses électrons dans ses couches électroniques :
Chaque couche électronique (de numéro « n » ) d’un atome est associée à une énergie (notée En) et correspond à un « niveau d’énergie »
Par exemple, la première couche de l’atome (n=1) est la plus proche du noyau et correspond au niveau d’énergie le plus bas, son énergie est notée E1.
Lorsque les électrons d’un atome occupent les couches électroniques les plus basses possibles alors l’atome est à son état d’énergie le plus bas : on dit qu’il est dans sont état fondamental.
Lorsque l’énergie électronique d’un atome est minimale alors il se trouve dans son état le plus stable appelé état fondamental.
Si un atome reçoit de l’énergie alors il peut passer à un niveau d’énergie plus élevé : il passe dans un état excité.
Un atome qui n’est pas dans son état d’énergie le plus bas (état fondamental) est dans un état dit excité.
Les différents niveaux d’énergie d’un atome peuvent être représentés sur son diagramme d’énergie.
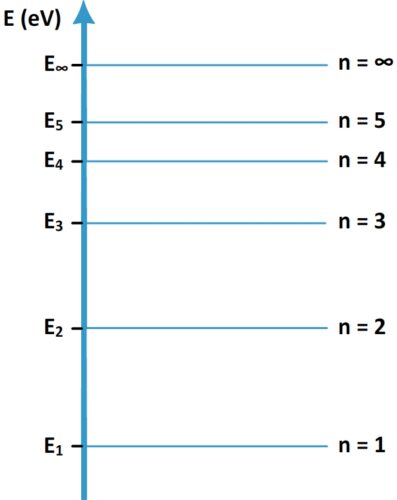
Diagramme d’énergie d’un atome
Qu’est ce qu’un diagramme d’énergie d’atome ?
Définition : Le diagramme d’énergie d’un atome est une figure indiquant les niveaux d’énergie de cet atome.
Quels sont éléments à représenter sur un diagramme d’énergie ?
Ce diagramme comporte toujours :
- Un axe vertical gradué orienté vers le haut
- La grandeur indiquée par cet axe (l’énergie)
- L’unité de cette énergie (l’électronvolt – eV)
- Les énergies des différents niveau ((E1, E2…)
- Les principaux niveaux d’énergie représentés par des traits horizontaux
- Les numéro des différents niveau d’énergie (n=1 , n = 2 etc)
- Le dernier niveau d’énergie (le plus élevé) correspondant à une couche n = ∞ (infini) d’énergie E∞ = 0 eV
On peut ajouter sur le diagramme :
- Les électrons sur les niveaux qu’ils occupent
- Les transitions des électrons d’un niveau vers un autre.
A quoi correspond le dernier niveau d’énergie n = ∞ ?
Il s’agit de la limite de l’atome, un électron qui atteint cette couche est éjecté de l’atome.
Quelques points importants :
- Etant donné que le niveau d’énergie de la couche la plus haute (n = ∞) correspond à une énergie nulle (E∞ = 0 eV), les autres niveaux ont une énergie inférieure négative.
- Il existe une infinité de niveaux d’énergie et seule une partie d’entre eux est représentée sur le diagramme d’énergie d’un atome.
- Plus les niveaux sont élevés (plus « n » est grand) et plus ils sont proches (la différence d’énergie entre deux niveaux consécutifs diminue).
Emission et absorption d’un photon par un atome
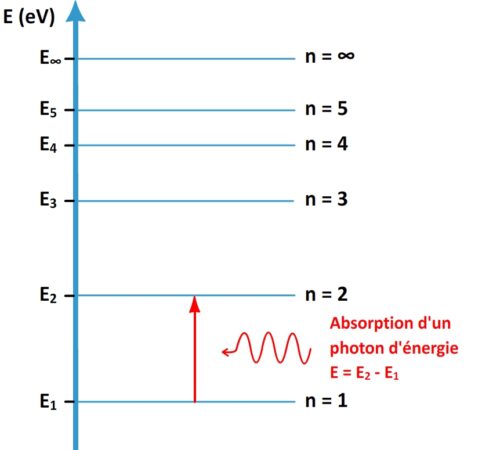
Absorption d’un photon
Un atome peut absorber un photon si l’énergie de ce dernier permet à un électron de l’atome de passer à un niveau d’énergie supérieur :
Si un photon possède une énergie « E » alors il peut être absorbé par un atome si cet atome possède un électron sur un niveau d’énergie « En » et qu’il existe un niveau d’énergie Em (avec Em > En ) tel que Em – En = E
Par conséquent un atome peut absorber les rayonnements dont la fréquence « ν » est telle qu’il existe deux niveaux d’énergie « n » et « «m » tels que h x ν = Em – En
Attention l’absorption n’est possible que si l’énergie du photon coïncide exactement avec l’écart d’énergie entre deux niveaux de l’atome : si l’énergie du photon est plus faible ou plus grande alors le photon ne peut pas être absorbé.
Le spectre d’absorption d’un atome résulte des absorptions qui se produisent lorsque les électrons d’un atome passent sur des niveaux supérieurs .
On peut déterminer le spectre d’absorption d’un atome en :
- cherchant les écarts d’énergie possibles entre les différents niveaux d’énergie de l’atome
- en déterminant la longueurs d’onde associée aux photons qui possèdent ces énergies grâce à la relation
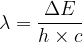
Sur le diagramme d’énergie d’un atome l’absorption d’un photon est représentée par une flèche montante indiquant la transition qu’effectue l’électron de son niveau initial vers son niveau final.
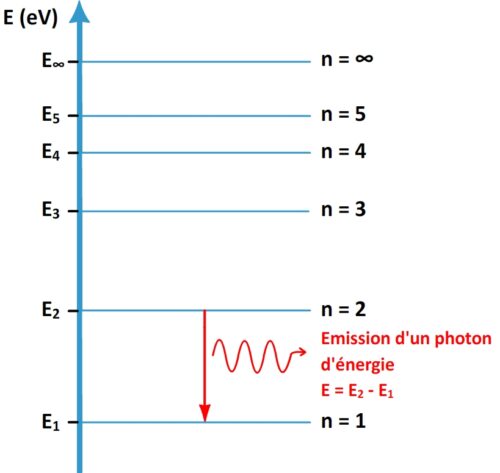
Emission d’un photon
Question : quelle est la condition pour qu’un atome puisse émettre un photon ?
Réponse : Un photon peut être émis par un atome dans un état excité, lorsqu’un électron passe vers un niveau d’énergie plus basse.
Si un électron passe d’un niveau d’énergie « m » à un niveau d’énergie « n » plus bas alors l’atome perd une énergie ΔE = Em – En. Cette énergie perdue est libérée sous la forme d’un rayonnement constitué d’un photon ayant une énergie ΔE .
D’après la relation de Planck-Einstein cette énergie est telle que ΔE = h x ν
La lumière émise possède une fréquence 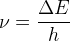
Sa longueur d’onde est donc 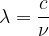 soit:
soit:
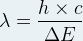
Sur le diagramme d’énergie d’un atome l’émission d’un photon est représentée par une flèche descendante indiquant la transition qu’effectue l’électron de son niveau initial vers son niveau final.
A réviser
Cours de seconde:
- Le cortège électronique de l’atome définit ses propriétés chimiques
- Vision et image
- Les spectres d’émission et d’absorption
Les autres cours de première spécialité
- Quantité de matière, masse molaire et concentration
- Réaction d’oxydoréduction et avancement
- Titrage colorimétrique redox
- Schéma de Lewis, géométrie, électronégativité et polarisation
- Cohésion des solides, dissolution, solubilité, hydrophilie et lipophilie
- Structure et nomenclature des espèces organiques
- Synthèses d’espèces organiques
- L’énergie de la matière organique
- Interactions, champs électrostatiques et gravitationnels
- Statique des fluides
- Variations du vecteur vitesse
- Courant électrique et bilans énergétiques
- Energies cinétiques, potentielles et mécaniques
- Les ondes mécaniques
- Images et couleurs
REVISER – AUTRES COURS DE PREMIERE SPECIALITE – APPROFONDIR ET DECOUVRIR
Pour approfondir et découvrir
- La dualité onde-corpuscule – sur Wikipedia
- La découverte de l’effet photoélectrique – Document pdf CEGEP Sainte Foy
