Le rayonnement solaire

Cours de physique-chimie niveau – niveau lycée première – Programme d’enseignement scientifique – Partie 2 – Le Soleil, notre source d’énergie – 2.1 – Le rayonnement solaire

• Les réactions de fusion nucléaire dans le Soleil
• Nature de l’énergie libérée lors d’une fusion nucléaire
• Relation d’Einstein ou relation d’équivalence masse-énergie
• Déterminer la variation de masse d’un système
• Variation de masse du Soleil
• Modélisation du Soleil par un corps noir
• Profil spectral du Soleil
• La Loi de Planck
• La loi de Wien
• Energie solaire reçue par la surface terrestre
• Variations de l’énergie lumineuse reçue par la surface terrestre

Les cours de seconde à réviser avant : Le noyau de l’atome, siège de sa masse et de son identité – Les transformations nucléaires – Vision et image

Les réactions de fusion nucléaire dans le Soleil

Le Soleil, comme toutes les étoiles, tire son énergie des réactions de fusion nucléaire dont il est le siège.

Les principales réactions de fusions nucléaires, qui se produisent au coeur du Soleil, font intervenir des noyaux d’hydrogène (élément majoritaire du Soleil à près de 73,5%).

Il se produit principalement un enchaînement de trois fusions nucléaires

• étape 1 : la fusion de deux noyaux d’hydrogène 1 conduit à la formation d’un noyau d’hydrogène 2 (deutérium), d’un positon (e⁺) ainsi que d’un neutrino (ν)

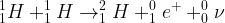
• étape 2 : la fusion d’un noyau d’hydrogène 2 (produit lors de l’étape 1) avec un noyau d’hydrogène 1 XXX forme un noyau d’hélium 3 et libére un rayonnement gamma (γ)

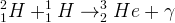
• étape 3 : la fusion de deux noyaux d’hélium 3 (formés lors de l’étape 2) forme un noyau d’hélium 4 et deux hydrogènes 1

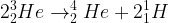
Le bilan de cette série de 3 fusions nucléaires peut s’écrire de la manière suivante :

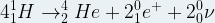
Remarque

Le bilan de ces transformations nucléaires faire apparaître deux particules « inhabituelles » : un positon (ou positron) et un neutrino.

• Un neutrino (symbole 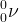) est une particule supposée sans masse et sans charge électrique de la même famille que l’électron (il s’agit d’un lepton) qui se déplace à la vitesse de la lumière.
• Un positon (symbole 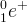) est une particule d’antimatière, c’est l’antiparticule de l’électron de même masse que lui mais avec une charge électrique élémentaire positive.

Nature de l’énergie libérée lors d’une fusion nucléaire

Toute énergie libérée lors d’un phénomène résulte nécessairement de la conversion d’une autre forme d’énergie (puisque l’énergie se conserve).

Dans le cas des réactions de fusion nucléaire c’est une partie de la masse des noyaux réactifs qui est convertie en énergie de rayonnement .

La masse totale des noyaux et particules formés lors des réactions de fusion est inférieure à la masse des noyaux réactifs.

On peut dire qu’il y a équivalence entre masse et énergie : La masse peut être convertie en énergie et inversement l’énergie peut aussi être convertie en masse.

La conversion masse-énergie est décrite par la relation d’Einstein (voir paragraphe suivant)

Relation d’Einstein ou relation d’équivalence masse-énergie

La relation d’Einstein, comme son nom l’indique, a été formulée par Albert Einstein, elle s’exprime par la célèbre relation :

E = m.c²

où :

• “m” est la masse du système étudié en kilogramme (kg)
• “c” est la célérité d’une onde électromagnétique dans le vide ( c = 3,00.10⁸ m.s^-1)
• “E” est l’énergie équivalente à la masse « m » en Joule (J)

La relation d’Einstein indique que l’énergie de masse « E » d’un système est proportionnelle à sa masse « m »

Dans le cas où un système subit une variation de masse Δm alors cette variation de masse correspond à une variation d’énergie ΔE qui peut s’exprimer grâce à la relation :

ΔE = Δm.c²

où :

• Δm = m(finale) – m(initiale)
• ΔE = E(finale) – E(initiale)

Les unités restent les mêmes ( variation d’énergie en Joule, variation de masse en kilogramme, célérité « c » en mètre par seconde).

Il est possible d’utiliser cette relation en exprimant les variations ΔE et Δm sous forme de valeurs absolues tout en précisant si la masse et l’énergie sont « gagnées » ou « perdues » par le système :

|ΔE| = |Δm|.c²

On peut également exprimer les variations sous forme algébrique en leur associant un signe positif ou négatif :

• Si l’énergie ou la masse du système augmente (gain de masse ou d’énergie) alors le signe de la variation est positif.
• Si l’énergie ou la masse du système diminue (perte de masse ou d’énergie) alors le signe de la variation est négatif.

Déterminer la variation de masse d’un système

L’expression de la relation d’Einstein peut être modifiée afin d’obtenir la variation de masse Δm d’un système échangeant une énergie ΔE :

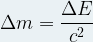
Variation de masse du Soleil

La puissance totale dissipée par le Soleil sous forme de rayonnement est

P_Soleil = 3,8.10²⁶ W

Il est possible de déterminer l’énergie dissipée par le Soleil à partir de la formule exprimant l’énergie échangée en fonction de la puissance :

E = P x Δt

Pendant une seconde l’énergie libérée par le Soleil sous forme de rayonnement est donc :

E = P x Δt

E = P_Soleil x Δt

E = 3,8.10²⁶ x 1

E = 3,8.10²⁶ J

Pendant une seconde la variation d’énergie du Soleil est donc ΔE = -3,8.10²⁶ J (le signe est négatif car cette énergie est perdue par le système Soleil.

D’après la relation d’Einstein :

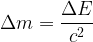
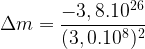
Δm = -4,2.10⁹ kg

A chaque seconde le Soleil convertit donc une masse de 4,2.10⁹ kg (4,2 millions de tonnes) en rayonnement.

Cette masse peut sembler énorme à l’échelle humaine mais elle est très faible en comparaison de la masse totale du Soleil qui est de 2,0.10³⁰ kg ( cela ne représente que 2,1.10^-19 % !)

Modélisation du Soleil par un corps noir

Un corps noir est un système qui n’émet de la lumière que du fait de sa température.

Remarque

Malgré son nom un corps noir n’est pas nécessairement noir ! Il peut aussi s’agir, par exemple d’un corps incandescent.

Le Soleil et les étoiles en général peuvent être décrits par le modèle du corps noir.

Profil spectral du Soleil

Le profil spectral est une courbe qui indique la répartition de la puissance lumineuse d’un rayonnement en fonction de la longueur d’onde (λ).

La grandeur indiquée en abscisse est souvent la luminance ou l’irradiance

il s’agit d’une courbe présentant un maximum à une longueur d’onde notée λ_max et appelée « longueur d’onde du maximum d’émission »

Exemple

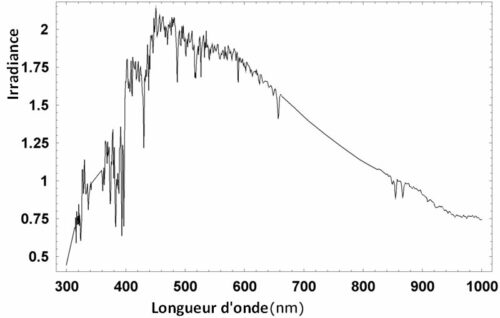
Le Soleil peut être modélisé par un corps noir avec un profil spectral dont la longueur d’onde du maximum d’émission vaut λ_max= 500 nm

La loi de Planck

Elle permet d’établir une relation entre la longueur d’onde du maximum d’émission ( λ_max) de la lumière émise par un corps noir et la température de surface de ce dernier.

D’après la loi de Planck λ_max dépend de la température de surface du corps noir émetteur :

• Plus un corps noir possède une température de surface élevée et plus λ_max est faible.
• Inversement, plus un corps noir possède une température basse et plus λ_max est élevée.

La loi de Planck permet (entre autres) de comparer la température de surface de deux étoiles à partir de leur couleur. En effet, la longueur d’onde d’une lumière visible va environ de 400 nm à 800 nm. La longueur d’onde est donc croissante suivant l’ordre de couleur violet, bleu, vert, jaune, orange rouge.

Par conséquent :

• à partir de la couleur de deux étoiles on peut comparer leur longueur d’onde du maximum d’émission (λ_max) ( une lumière rouge a un λ_max supérieur à celui d’une lumière jaune qui a elle-même un λ_max supérieur à celui d’une lumière verte etc)
• La comparaison des longueurs d’onde du maximum d’émission permet (grâce à la loi de Planck) de comparer leur température de surface.

En particulier :

• Les étoiles les plus chaudes émettent une lumière bleue-violette (longueurs d’onde minimales du visible)
• Les étoiles les moins chaudes émettent une lumière rouge (longueurs d’onde maximales du visible)

La loi de Wien

La loi de Wien est une relation entre la longueur d’onde du maximum d’émission d’un corps noir (λ_max) et sa température de surface.

On l’exprime le plus souvent grâce à la formule :

λ_max x T = 2,89.10^-3

où :

• λ_max est exprimée en mètre (m)
• T est exprimée en Kelvin (K)

La loi de Wien permet d’exprimer la température de surface d’un corps noir à partir de la longueur d’onde du maximum d’émission :

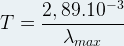
Elle permet aussi d’exprimer la longueur d’onde du maximum d’émission (λ_max) en fonction de la température :

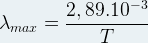
Si l’on applique la loi de Wien au Soleil alors on peut déterminer sa température de surface :

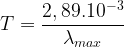
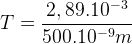
T = 5780 K

La température de surface du Soleil est proche de 5780 K.

Energie solaire reçue par la surface terrestre

Le Soleil émet son rayonnement avec une puissance P = 3,8.10²⁶ W dans toutes les directions de l’espace. On peut considérer que cette puissance se répartit sur une sphère dont le rayon croit avec la distance au Soleil.

Au niveau de la Terre cette puissance se répartit sur une sphère dont le rayon correspond à la distance Soleil-Terre. La valeur moyenne de cette distance étant d = 1,5.10¹¹ m, on peut considérer qu’au niveau de la Terre la puissance émise par le Soleil se répartit sur une sphère de surface totale :

S = 4.π.d²

S = 4.π.(1,5.10¹¹)²

S = 2,8.10²³ m²

Au niveau de la Terre chaque faisceau lumineux de section 1 m² transmet donc une puissance :

P_terre = Psoleil / S

P_terre = 3,8.10²⁶ / 2,8.10²³

P_terre = 1357 W/m²

Chaque faisceau lumineux de section 1 m² transmet donc à la une puissance de 1357 W

Cela signifie que si une surface intercepte un faisceau lumineux de section 1 m² alors elle reçoit une puissance de 1357 W. Ce sera le cas pour une surface terrestre de 1 m² si elle est perpendiculaire à la direction de propagation des rayons lumineux.

Une surface « S » perpendiculaire aux rayons lumineux recevra donc une puissance :

P = S x 1357 (avec P en watt et S en m² )

Si l’on note «θ » (théta) l’angle entre la normale à la surface terrestre (droite perpendiculaire à cette surface) alors la puissance reçue par cette surface devient :

P = S x 1357 x cos (θ )

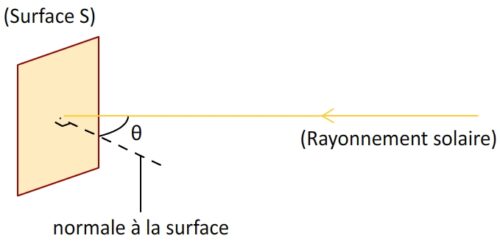
Cas extrêmes :

• Si θ =0 alors les rayons lumineux sont perpendiculaires à la surface, puisque cos (0) = 1 alors P = S x 1357 x 1 = S x 1357. Cette situation est possible au niveau de l’équateur vers midi.

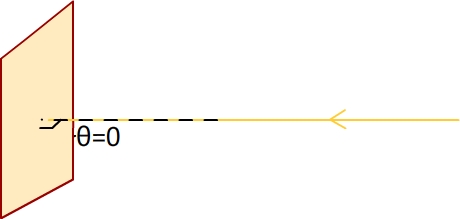
• Si θ = 90°alors les rayons lumineux sont parallèles à la surface, puisque cos (90) = 0 alors P = S x 1357 x 0 = 0 c’est à dire que la puissance reçue est nulle. On s’approche de cette situation au moment du levé du Soleil et à son coucher.

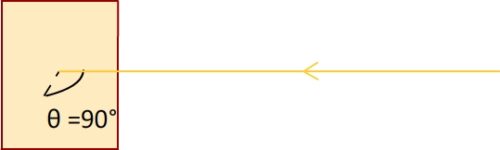
• Si 0 <θ  <90°alors la puissance reçue est comprise entre 0 et 1357 W. Plus l’angle est petit, plus la puissance reçue est faible.

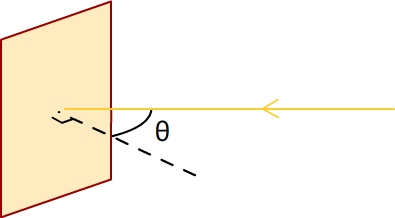
La puissance reçue par une surface terrestre dépend de l’angle que forme sa normale avec les rayons lumineux.

Variations de l’énergie lumineuse reçue par la surface terrestre

La puissance lumineuse reçue par une surface terrestre dépend de l’angle que forme sa normale avec les rayons lumineux. Tout facteur associé à une variation de cet angle est donc aussi responsable d’une variation de la puissance reçue.

Cette variation se fait :

• en fonction de la latitude
• au cours d’une journée
• au cours de l’année

Variation en fonction de la latitude

En suivant un même méridien l’angle « θ » de la normale varie :

• il augmente en se rapprochant d’un pôle (nord au sud)
• il diminue en se rapprochant de l’équateur

Cette variation explique que les zones polaires (qui reçoivent l’énergie solaire la plus faible) soient plus froides que les zones équatoriales (qui reçoivent l’énergie lumineuse maximale)

Variations au cours d’une journée

• La nuit

La surface terrestre se trouve sur la face non éclairée de la Terre, la puissance du rayonnement solaire reçu est donc nulle.

• L’aube

En début de journée le Soleil se lève à l’est, les rayons lumineux sont « rasants », ils sont presque parallèles à la surface terrestre, l’angle de ces rayons par rapport à la normale est proche de « 90° » par conséquent la puissance reçue est très faible.

• La matinée (de l’aube à midi)

Le Soleil s’élève dans le ciel, l’angle des rayons lumineux par rapport à la normale diminue et la puissance du rayonnement solaire reçue par la surface terrestre augmente progressivement.

• Midi

Le Soleil atteint le zénith (point le plus haut dans le ciel) et l’angle « θ » est alors minimal tandis que la puissance solaire est quant à elle maximale.

• Après-midi

Le Soleil semble « descendre » vers l’horizon, l’angle «  θ » augmente tout au long de l’après midi et la puissance du rayonnement solaire reçu diminue.

• Crépuscule

Le Soleil est à nouveau proche de l’horizon, les rayons lumineux sont « rasants » par rapport à la surface terrestre et l’angle «  θ » tend vers « 90° » par conséquent la puissance du rayonnement solaire reçue se rapproche de « 0 »

En résumé :

La puissance du rayonnement solaire reçu par une surface terrestre est nulle pendant la nuit, augmente ensuite à partir de l’aube jusqu’à atteindre son maximum à midi. Elle diminue ensuite pendant l’après midi jusqu’à redevenir nulle après le coucher du Soleil.

Exercices corrigés et sujets pour le chapitre “Le rayonnement solaire”

Evaluation commune, exercice corrigé “Le rayonnement solaire reçu sur Terre”