Exercice 1: LE RAYONNEMENT SOLAIRE REÇU SUR TERRE

Correction de la question 1
D’après l’énoncé la loi de Wien permet d’obtenir la relation suivante:
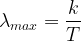 avec k = 2,89.10-3
avec k = 2,89.10-3
Pour déterminer la température de surface du Soleil il faut dans un premier temps exprimer la température en fonction des autres grandeurs de cette relation:
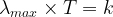
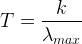
Pour calculer la température (T) nous avons besoins de la valeur de la longueur d’onde d’émission maximale λmax.
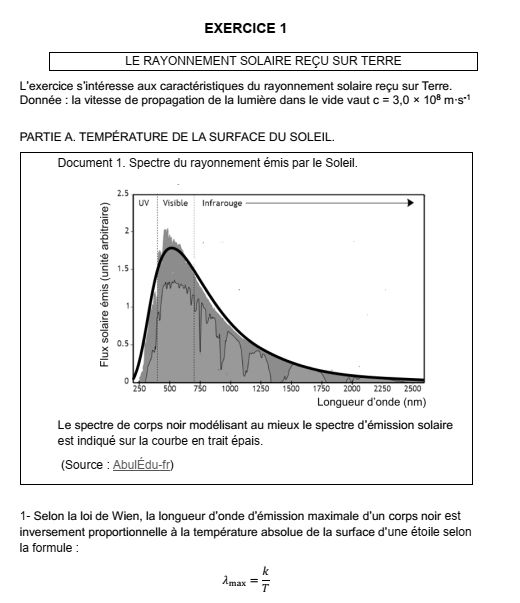
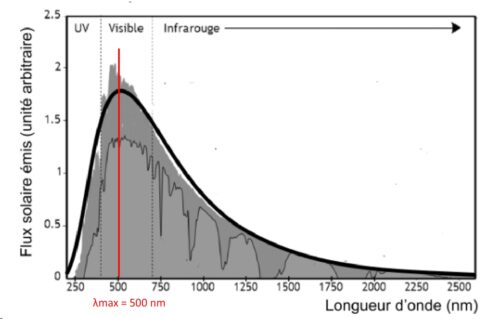
On peut la déterminer à partir de du profil spectral fourni dans le document 1 du sujet,
Cette courbe comporte aussi le spectre obtenu en modélisant le Soleil par un corps noir, elle est plus facilement exploitable. D’après cette courbe λmax = 500 nm
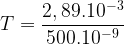
T = 5780 K
Soit en dergré Celsius
ϴ = 5780 – 273
ϴ = 5507 °C

Correction
La relation entre la distance de propagation (d) la célérité (c) et la durée de propagation Δt est:
d = c x Δt
La célérité de la lumière dans le vide est c = 3,0.108 m.s-1 et d’après l’énoncé la lumière met une durée Δt = 500 s pour se propager du Soleil à la Terre.
d = 3,0.108 x 500
d = 1,5.1011 m
La distance moyenne Terre-Soleil est donc bien de 1,5.1011 m

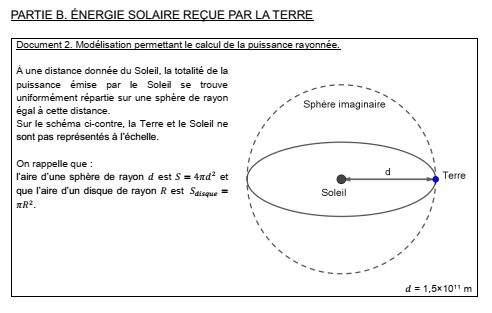
La constante solaire correspond à la puissance du rayonnement interceptée par une surface de 1 m2 mais le Soleil émet ses rayonnements dans toutes les directions autour de lui et sa puissance rayonnée , à un instant donnée, se répartit sur une sphère dont il est le centre.
Pour déterminer la puissance totale rayonnée par le Soleil il suffit de déterminer la surface totale sur laquelle se répartit ce rayonnement et de la multiplier par la puissance reçue par chaque mètre carré de cette surface:
P(Soleil) = S(sphère) x P(1m2)
P(Soleil) = 4 x π x d2 x P(1m2)
P(Soleil) = 4 x π x (1,5.1011) x 1370
P(Soleil) = 3,87.1026 W
La puissance totale rayonnée par le Soleil est donc de 3,87.1026 watt

L’aire d’un disque de rayon R peut être calculée grâce à la relation
S(disque) = π x R2
Dans ce cas le rayon est celui de la Terre, c’est à dire 6400 km (6,400.106 m)
S(disque) = π x (6,400.106 )2
S(disque) =1,29.1014 m2

La Terre intercepte un faisceau de rayonnements dont la section est égale à la surface calculée dans la question précédente. Chaque mètre carré de cette section transmet une puissance de 1370 W par conséquent la puissance du rayonnement intercepté par la Terre correpsond à:
P(Terre) = S(disque) x P(1m2)
P(Terre) = 1,29.1014 x 1370
P(Terre) = 1,77.1017 W
D’après ce modèle on arrive donc bien à démontrer que la puissance du rayonnement solaire intercepté par la Terre est d’environ 1,77.1017 W

L’inclinaison de la surface terrestre varie en fonction de la latitude, au niveau niveau de l’équateur la surface terrestre est perpendiculaire à la direction de propagation des rayons lumineux mais plus on se rapproche des pôles et plus l’angle entre les rayons lumineux et la surface terrestre diminue.
Par conséquent la section du faisceau lumineux intercepté par une surface terrestre d’un mètre carré est d’un mètre carré au niveau de l’équateur mais cette section diminue d’autant plus que cette surface terrestre est proche du pôle nord ou du pôle sud
Voir aussi de le cours “Le rayonnement solaire“
