Enseignement scientifique de première – Partie 4 – Son et musique, porteurs d’information – 4.2 – La musique ou l’art de faire entendre les nombres
- Les notes de musique
- Les intervalles
- Intervalles consonants et intervalles dissonants
- Les quintes
- Les octaves
- Les gammes
- La gamme naturelle de Pythagore
- Exemple : construction de la deuxième octave de la gamme de Pythagore
- La quinte du loup
- La gamme tempérée
Les notes de musique
Chaque note de musique est définie à partir de sa fréquence fondamentale et de la fréquence de ses harmoniques.
Par exemples
- la note « la » de l’octave 3 (noté la3) a pour fréquence fondamentale f0 = 440 Hz
- la note « do » de l’octave 0 (notée do0) a pour fréquence fondamentale f0 = 32,70 Hz
La fréquence fondamentale d’une note dépend :
- de l’octave à laquelle elle appartient
- de la gamme dont elle fait partie
Les intervalles
Définition
L’intervalle de deux notes est le rapport des fréquences de ces deux notes.
Si par exemple une note est caractérisée par une fréquence f1= 1046.5 Hz et une autre note par une fréquence f2= 2093.0 Hz alors l’intervalle de ces deux notes correspond au rapport :
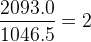
Intervalles consonants et intervalles dissonants
Pour qu’un intervalle soit consonant, il doit correspondre à un rapport simple, c’est à dire qu’il peut être exprimé comme une fraction de deux nombres entiers : 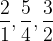 …
…
En musique on considère que les intervalles les plus consonants sont l’octave et la quinte.
Intervalle consonant
Lorsque l’enchaînement de deux notes « sonne bien », c’est à dire qu’il peut être considéré comme harmonieux, alors l’intervalle de ces deux notes est qualifié de consonant.
Intervalle dissonant
Dans le cas contraire, si l’enchaînement de deux notes semble « désagréable », s’il ne « sonne pas bien » alors on qualifie cet intervalle de dissonant
Des intervalles consonants permettent d’enchaîner deux notes comportant des harmoniques communes.
Les principaux intervalles consonants :
| Intervalle | Rapports |
| Unisson | 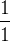 (1) (1) |
| Tierce mineure | 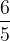 (1,2) (1,2) |
| Tierce majeure | 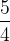 (1,25) (1,25) |
| Quarte | 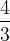 (1,33) (1,33) |
| Quinte | 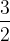 (1,5) (1,5) |
| Sixte mineure | 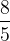 (1,6) (1,6) |
| Sixte majeure | 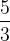 (1,66) (1,66) |
| Octave | 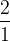 (2) (2) |
Les quintes
Les quintes et les octaves sont les principaux intervalles consonants, ce sont les deux intervalles qu’il est nécessaire de connaître par coeur !
On retient donc :
Une quinte est un intervalle de 3/2, il correspond donc à l’enchaînement de deux notes avec un rapport de 3/2 (1,5).
Si l’on enchaîne une note de fréquence fondamentale f1 puis une note de fréquence fondamentale f2 alors :
l’intervalle est une quinte montante si 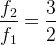
l’intervalle est une quinte descendante si 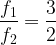 (ou
(ou 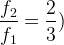
Comment savoir si l’enchaînement de deux notes constitue une quinte ?
Il suffit diviser la fréquence la plus élevée par le fréquence la plus basse et vérifier que le résultat donne 1,5 (pour une quinte parfaite) ou une valeur très proche (pour une quinte approchée).
Exemple
Les notes de fréquences f1 = 264 Hz et f2 = 396 Hz forment une quinte car :
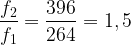
Les principaux enchaînement de notes constituant des quintes :
- do et sol (d’une même octave)
- do# et sol# (d’une même octave)
- ré et la (d’une même octave)
- mib et sib (d’une même octave)
- mi et si (d’une même octave)
- fa d’une octave et do de l’octave suivante (par exemple fa1 et do2 ou fa2 et do3 etc)
- fa# d’une octave et do# de l’octave suivante (par exemple fa#1 et do#2 ou fa#2 et do#3 etc)
- sol d’une octave et ré de l’octave suivante (par exemple sol1 et ré2 ou sol2 et ré3 etc)
- sol# d’une octave et mib de l’octave suivante (par exemple sol#1 et mib2 ou sol#2 et mib 3 etc)
- la d’une octave et mi de l’octave suivante (par exemple la1 et mi2 ou la2 et mi3 etc)
- la# d’une octave et fa de l’octave suivante (par exemple la#1 et fa2 ou la#2 et fa3 etc)
- si d’une octave et fa# de l’octave suivante (par exemple si1 et fa#2 ou si2 et fa#3 etc)
Les octaves
Définition
Deux notes forment un intervalle d’une octave si leur fréquence fondamentale f1 et f2 ont un rapport de valeur « 2 »
Si deux notes forment une octave alors l’une des deux notes possède une fréquence fondamentale deux fois plus élevée que l’autre.
Exemples
une note de fréquence f1 = 440 Hz et une note de fréquence f2 = 220 Hz forment une octave car
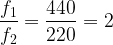
Une note de fréquence f1 = 130,8 Hz et une note de fréquence f2 = 261,6 Hz forment une octave car 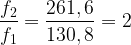
Une note d’une octave et la note de l’octave suivante forment toujours une octave : le do1 et le do2, le do2 et le do3, le fa4 et le fa5, le sol2 et le sol3 etc….
Les gammes
Définition
Une gamme est un ensemble de notes utilisées pour composer une musique.
La plupart des gammes répartissent leur notes sur un intervalle d’une octave :
- Une note de fréquence f1 constitue la limite inférieure de l’octave et correspond à la première note de la gamme.
- Une note de fréquence f2 constitue la limite supérieure de l’octave (et constitue la première note de l’octave suivante).
- Puisque ces deux notes de fréquence f1 et f2 forment une octave f2 = 2 x f1
- Les autres notes de la gamme ont toutes une fréquence comprises entre ces deux valeurs limites (f1 et 2f1), elles dont définies en choisissant un intervalle (souvent la quinte) à partir de la première note de l’octave.
Les deux principales gammes sont :
- la gamme naturelle de Pythagore
- la gamme tempérée
La gamme naturelle de Pythagore
C’est une gamme dont on attribue l’interprétation au célèbre mathématicien et savant grec Pythagore.
Elle est composée d’un cycle d’octaves
Les notes d’une octave ont donc toutes leur fréquence comprise entre :
- une fréquence f0 qui correspond à la fréquence de la première note de l’octave (une note « do »)
- et une fréquence 2 x f0 qui marque la fin de l’octave et correspond à la première note de l’octave suivante.
Chaque note d’une octave forme une quinte avec au moins l’une des autres note de l’octave.
Règles suivies pour déterminer les fréquences des notes d’une octave de la gamme naturelle de Pythagore :
- Le début de l’octave : une première note (en général un « do ») de fréquence f0 est choisie comme début de l’octave.
- La fin de l’octave : on détermine la borne supérieure de cette octave en multipliant la fréquence de la première note par 2 : 2 x f0.
- Trouver la fréquence de la note suivante en multipliant par une quinte: on détermine la fréquence de chaque note en multipliant la fréquence de la précédente par une quinte, c’est à dire par 3/2, puis l’on vérifie que la valeur obtenue ne dépasse pas la limite 2 x f0.
- Vérifier que la limite supérieure de l’octave n’est pas dépassée : si la limite n’est pas dépassée alors la fréquence obtenue est bien celle d’une note de l’octave.
- Ramener (si nécessaire) la fréquence dans les limite de l’octave : si la limite est dépassée on divise la valeur obtenue par « 2 » autant de fois que nécessaire pour obtenir une valeur ne dépassant pas la limite supérieure de l’octave.
- Terminer l’octave : la gamme peut être considérée comme complète lorsque la fréquence calculée est très proche de la limite de l’octave (2 x f0). (cette limite peut être atteinte au bout de la 6ème, de la 8ème ou de la 13ème fréquence et permet de définir des gammes à 5, 7 ou 8 notes)
- Associer chaque fréquence à une note : les fréquences obtenues doivent être classée par ordre croissant afin de pouvoir les associer à une note.
La dernière quinte de l’octave d’une gamme naturelle de Pythagore est appelée quinte du Loup
En effet cette dernière quinte est légèrement raccourcie afin de faire coïncider la fin d’une octave avec le début de la suivante. La quinte qui correspond à l’enchaînement du« Fa » d’une octave et du « Do » de l’octave suivante est donc plus courte (le rapport des fréquences est légèrement plus petit que 3/2) et semble dissonante (une dissonance qui peut évoquer un hurlement de loup!).
La gamme naturelle de Pythagore a donc l’avantage d’être basée sur une majorité de quintes rigoureusement exacte mais elle présente l’inconvénient de comporter une quinte du loup (dissonante) à la fin de chaque octave.
La gamme de Pythagore peut être pentatonique, heptatonique ou chromatique
- En effet la gamme pentatonique se limite à 5 notes : do, ré, mi, sol, la
- Une gamme heptatonique comporte 7 notes : do, ré, mi, fa, sol, la, si
- Une gamme chromatique comprend 12 notes : do, do# (do dièse), ré, mib (mi bémol), mi, fa, fa# (fa dièse), sol, sol# (sol dièse), la, sib (si bémol), si
Exemple : construction de la deuxième octave de la gamme de Pythagore
Le «Do » de l’octave 2 a pour fréquence f0 = 130,8 Hz
Cette octave s’étend donc jusqu’à une fréquence 2 x f0 = 2 x 130,8 soit 261,6 Hz. Cette Fréquence limite correspond aussi au « Do » de l’octave 3.
Fréquences des notes de la gamme
- La fréquence « 0 » f0
C’est celle du Do : f0 = 130,8 Hz
- Calcul de f1
f1 = f0 x (3/2)
f1 = 130,8 x (3/2)
f1 = 196,2 Hz (cette valeur est inférieure à la limite de 261,6 Hz)
- Calcul de f2
f2 = f1 x (3/2)
f2 = 196,2 x (3/2)
f2 = 294,3 Hz .
La limite (261,6 Hz) est dépassée, cette valeur est donc divisée par « 2 » :
294,3:2= 147,15 Hz (valeur inférieure à la limite 261,6 Hz)
f2 = 147,15 Hz
- Calcul de f3
f3 = f2 x (3/2)
f3 = 147,15 x (3/2)
f3 = 220,725 Hz (valeur inférieure à la limite 261,6 Hz)
- Calcul de f4
f4 = f3 x (3/2)
f4 = 220,725 Hz x (3/2)
f4 = 331,087 Hz
La limite (261,6 Hz) est dépassée, cette valeur est donc divisée par « 2 »
331,087:2 = 165,544 Hz (valeur inférieure à la limite 261,6 Hz)
f4 = 165,544 Hz
- Calcul de f5
f5 = f4 x (3/2)
f5 = 165,544 x (3/2)
f5 = 248,316 Hz (valeur inférieure à la limite 261,6 Hz)
- Calcul de f6
f6 = f5 x (3/2)
f6 = 248,316 x (3/2)
f6 =372,473 Hz
La limite (261,6 Hz) est dépassée, cette valeur est donc divisée par « 2 »
372,54:2 = 186,27 Hz (valeur inférieure à la limite 261,6 Hz)
f6 = 186,237 Hz
- Calcul de f7
f7 = f6 x (3/2)
f7 = 186,237 x (3/2)
f7 = 279,355 Hz
La limite (261,6 Hz) est dépassée, cette valeur est donc divisée par « 2 »
279,355:2 = 139,678 Hz (valeur inférieure à la limite 261,6 Hz)
f7 = 139,678 Hz
- Calcul de f8
f8 = f7 x (3/2)
f8 = 139,678 x (3/2)
f8 = 209,516 Hz (valeur inférieure à la limite 261,6 Hz)
f8 = 209,516 Hz
- Calcul de f9
f9 = f8 x (3/2)
f9 = 209,516 x (3/2)
f9 = 314,274 Hz
La limite (261,6 Hz) est dépassée, cette valeur est donc divisée par « 2 »
314,274:2 = 157,137 Hz (valeur inférieure à la limite 261,6 Hz)
f9 = 157,137 Hz
- Calcul de f10
f10 = f9 x (3/2)
f10 = 157,137 x (3/2)
f10 = 235,706 Hz (valeur inférieure à la limite 261,6 Hz)
f10 = 235,706 Hz
- Calcul de f11
f11 = f10 x (3/2)
f11 = 235,706 x (3/2)
f11 = 353,559 Hz
La limite (261,6 Hz) est dépassée, cette valeur est donc divisée par « 2 »
353,559:2 = 176,779 Hz (valeur inférieure à la limite 261,6 Hz)
f11 = 176,779 Hz
- Calcul de f12
f12 = f11 x (3/2)
f12 = 176,779 x (3/2)
f12 = 265,169 Hz
Cette treizième fréquence, très proche de la fin de l’octave 2 (à 261,6 Hz) est raccourcie et ramenée à 261,6 Hz afin de que l’octave 2 se termine précisément là où commence l’octave suivante.
Finalement la fréquence f12 de l’octave 2 a pour valeur f12 = 261,6 Hz et correspond au Do de l’octave suivante (l’octave 3) de fréquence f0 = 261,6 Hz
La gamme de Pythagore comprend donc les notes dont les fréquences, classées de manière croissantes, sont :
f0 = 130,8 Hz
f7 = 139,678 Hz
f2 = 147,15 Hz
f9 = 157,137 Hz
f4 = 165,544 Hz
f11 = 176,779 Hz
f6 = 186,237 Hz
f1 = 196,2 Hz
f8 = 209,516 Hz
f3 = 220,725 Hz
f10 = 235,706 Hz
f5 = 248,316 Hz
Sachant que les notes sont nommées (dans l’ordre) Do – Do♯ – Ré – Mib– Mi – Fa – Fa♯ – Sol – Sol♯ – La – Sib – Si, on peut associer chaque note de l’octave 2 à sa fréquence :
| Notes de l’octave 2 | Fréquence en Hertz (Hz) |
| Do | 130,8 |
| Do♯ | 139,678 |
| Ré | 147,15 |
| Mib | 157,137 |
| Mi | 165,544 |
| Fa | 176,779 |
| Fa♯ | 186,237 |
| Sol | 196,2 |
| Sol♯ | 209,516 |
| La | 220,725 |
| Sib | 235,706 |
| Si | 248,316 |
La gamme naturelle de Pythagore présente l’avantage de comporter une majorité de quintes justes mais a l’inconvénient de finir chaque octave par une quinte légèrement fausse (donc dissonante) appelée quinte du loup.
Elle est restée en usage jusqu’à la renaissance et l’invention de la gamme tempérée
La quinte du loup
Elle correspond à la dernière quinte d’une octave, c’est à dire l’enchaînement de la note « Fa » d’une octave et de la note « Do » de l’octave suivante.
Le rapport des fréquences de ces deux notes est légèrement inférieur à la valeur d’une quinte (1,5) car pour préserver le cycle des octaves (permettre à chaque octave de commencer là où finit la précédente) la dernière quinte a été raccourcie.
Par exemple l’intervalle Do3 (Do de l’octave 3) – Fa2 (Fa de l’octave 2) a pour valeur :
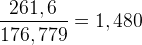
Ce qui correspond bien à une valeur approchée (mais par rigoureusement exacte!) de la quinte (1,5).
Cette quinte est donc légèrement fausse et laisse percevoir une dissonance peu agréable (qui pourrait évoquer le hurlement d’un loup!)
La gamme tempérée
Elle est définie à la renaissance par le mathématicien et scientifique néerlandais Simon Stevin, et reste la gamme la plus souvent utilisée de nos jours.

La gamme tempérée est divisée en octaves comportant chacune (comme la gamme naturelle chromatique de Pythagore) douze notes formant toutes des intervalles rigoureusement égaux proches de la quinte.
Si la fréquence de la première note d’une octave est f0 alors la fréquence de la première note de l’octave suivante a pour fréquence 2 x f0 et les notes de cette octave ont dont une fréquence comprise dans l’intervalle mathématique [ f0 ; 2 x f0 [
Si l’on note note « r » l’intervalle entre deux notes successives alors :
f1 = f0 x r
f2 = f1 x r = f0 x r x r = f0 x r2
f3 = f2 x r = f0 x r2 x r = f0 x r3
f4 = f3 x r = f0 x r3 x r = f0 x r4
etc.
Soit d’une manière générale :
fn = f0 x rn
Pour la douzième note on a donc les deux égalités :
f12 = f0 x r12 et f12 = f0 x 2 donc :
f0 x r12 = f0 x 2
r12 = 2
(r12 )1/12 = (2) 1/12
r12 x 1/12 = (2) 1/12
r = (2) 1/12 soit environ r = 1,05946
L’intervalle entre deux notes successives d’une octave de la gamme tempérée vaut donc r = 2 1/12
Pour obtenir les fréquences des douze notes d’une octave dont le Do a pour fréquence f0 il suffit d’utiliser la relation suivante :
fn = f0 x (2 1/12) n
Par exemple, pour la deuxième octave dont la note « Do » a pour fréquence f0 = 130,8 Hz:
f1 = 130,8 x (2 1/12) 1= 138,58 Hz
f2 = 130,8 x (2 1/12) 2= 146,82 Hz
f3 = 130,8 x (2 1/12) 3= 155,55 Hz
f4 = 130,8 x (2 1/12) 4= 164,80 Hz
f5 = 130,8 x (2 1/12) 5= 174,60 Hz
f6 = 130,8 x (2 1/12) 6= 184,98 Hz
f7 = 130,8 x (2 1/12) 7= 195,98 Hz
f8 = 130,8 x (2 1/12) 8= 207,63 Hz
f9 = 130,8 x (2 1/12) 9= 219,98 Hz
f10 = 130,8 x (2 1/12) 10= 233,06 Hz
f11 = 130,8 x (2 1/12) 11= 246,92 Hz
Les fréquences ainsi calculées peuvent être associées aux notes auxquelles elles correspondent :
| Notes de l’octave 2 | Fréquence en Hertz (Hz) |
| Do | 130,8 |
| Do♯ | 138,58 |
| Ré | 146,82 |
| Mib | 155,55 |
| Mi | 164,80 |
| Fa | 174,60 |
| Fa♯ | 184,98 |
| Sol | 195,98 |
| Sol♯ | 207,63 |
| La | 219,98 |
| Sib | 233,06 |
| Si | 246,92 |
Si l’on enchaine deux notes séparées de 7 intervalles « r » alors l’intervalle entre ces deux notes correspond à :
r7 = (2 1/12) 7
r7 = 1,498
On retrouve un intervalle correspondant quasiment à une quinte. La différence est minime par rapport à la quinte exacte et ne provoque de dissonance perceptible.
A réviser pour aborder ce cours
Cours de seconde:
Cours de première, enseignement scientifique:
Les autre cours de première, enseignement scientifique:
