Cours de physique-chimie | première spécialité
Ce cours correspond à la partie “Interactions fondamentales et introduction à la notion de champ” du programme de première spécialité.
Il est situé dans la partie du programme “Description d’un fluide au repos”
- Qu’est-ce qu’un fluide ?
- Température d’un fluide
- Pression d’un fluide
- Masse volumique d’un fluide
- Loi de Mariotte
- Forces pressantes
- Loi fondamentale de statique des fluides
REVISER – AUTRES COURS DE PREMIERE SPECIALITE – APPROFONDIR ET DECOUVRIR
Qu’est-ce qu’un fluide ?
Un fluide est un corps composé de particules pouvant de déplacer les unes par rapports aux autres. On retrouve cette propriété pour les états liquides et gazeux.
Un fluide est un liquide ou un gaz
Un fluide se caractérise par sa capacité à s’écouler, il peut être décrit par des grandeurs telles que:
- sa masse volumique
- sa température
- sa pression
Température d’un fluide
La température est une grandeur qui peut être exprimée dans deux échelles: l’échelle de température Celsius ou l’échelle de température Kelvin (et non pas Kevin!)
L’échelle de température Celsius
Dans cette échelle la température se note θ (lettre grecque thêta ) et s’exprime en degré Celsius de symbole “ °C “
Cette échelle été établie à partir deux températures “repère”: celle de la fusion de la glace pure (utilisée pour définir le zéro de cette échelle) et celle de l’ébullition de l’eau pure (utilisée pour définir la valeur “cent” )
L’échelle de température Kelvin
Dans cette échelle la température se note T (comme Température) et s’exprime en Kelvin de symbole ” K “
Comparaison des échelles de température Kelvin et Celsius
Ces deux échelles ont adopté le même système de division, il en résulte qu’une différence entre deux températures a même valeur: par exemple une différence de deux degrés Celsius correspond aussi à une différence de deux Kelvins, une différence de 15 Kelvins équivaut à une différence de 15 degrés Celsius etc…
Par contre ces deux échelles n’ont pas la même origine, leur point “zéro” n’est pas le même:
- l’origine de l’échelle Celsius est la température de la glace fondante (température de fusion de l’eau pure sous une pression d’une atmosphère)
- l’origine de l’échelle Kelvin correspond au “zéro absolu”, il s’agit la température la plus basse que la matière peut atteindre (absence totale d’agitation thermique)
Conversion de températures
Il existe un décalage de 273 entre les deux échelles de température, en effet le “zéro absolu” pris comme origine de l’échelle Kelvin correspond à une température de -273,15 °C.
Par conséquent, pour convertir une température en Kelvin il suffit de lui ajouter 273,15 (ou 273 si l’on souhaite arrondir à l’unité près).
La conversion des degrés Celsius vers les Kelvins peut se faire grâce à la relation suivante:
T (K) = θ (°C) + 273,15
où:
- T est la température en Kelvin
- θ est la température en degré Celsius
Par exemple:
- une température de 2°C correspond à T = 2 +273,15 soit 275,15 K
- une température de 10°C correspond à T = 10 +273,15 soit 283,15 K
La conversion des Kelvins vers les degrés Celsius se fait quant à elle en soustrayant 273,15 ce qui revient à utiliser la relation suivante:
θ (°C) = T (K) – 273,15
Par exemple:
- une température de 300 K correspond àθ = 300 – 273,15 = 26,85 °C
- une température de 220 K correspond àθ = 220 – 273,15 = -53,15 °C
Température et propriétés de la matière à l’échelle microscopique
La température reflète l’état d’agitation de la matière: plus l’agitation (dite “thermique”) des entités qui la composent est importante et plus sa température est élevée.
Inversement plus la température d’un corps croît et plus l’agitation des molécules, des atomes ou des ions est importante: leurs vitesses de déplacement et de vibration sont plus importantes.
La température d’un corps dépend de l’agitation de ses entités chimiques
Pression d’un fluide
Qu’est ce que la pression ?
Définition
La pression est une grandeur physique définie en tous points d’un fluide, elle exprime la poussée qui s’exerce au sein de ce fluide ou sur un corps avec lequel il est en contact.
Notation et unités
La pression se note “P” ( P comme Pression)
L’unité de pression du système international est le Pascal, de symbole Pa. (en hommage à Blaise Pascal)

D’autres unités de pression sont couramment utilisées et il est nécessaire de savoir les convertir en pascal:
- Le bar (symbole bar), 1 bar = 105 Pa (il correspond à une valeur aprochée de la pression atmosphérique moyenne qui vaut 101325 Pa)
- L ‘atmosphère (symbol atm), 1 atm 101325 Pa (valeur approchée 1,013.105 Pa)
La pression atmosphérique
Définition
On appelle “pression atmosphérique” la pression de l’air libre (la pression de l’air présent dans l’atmosphère)
La pression atmosphérique moyenne a une valeur de 101325 Pa
Cette valeur est susceptible de subir des variations et dépend de l’altitude.
Lorsqu’un liquide a une surface libre en contact avec l’air libre la pression à la surface de fluide correspond à la pression atmosphérique.
Pression et propriété de la matière à l’échelle microscopique
La pression traduit la poussée que peut exercer un fluide sur corps
Cette poussée résulte des collisions entre les molécules du fluide et la surface du corps.
Par conséquent plus les chocs moléculaires sont nombreux et violents et plus la pression est élevée.
Voir cours La pression dans les gaz et liquides
Masse volumique d’un fluide
La masse volumique d’un fluide:
- se note ρ (lettre grecque rho)
- s’exprime toujours en kilogramme par mètre cube (kg.m-3)
- peut se calculer grâce à la relation ρ = m / V
Lorsqu’un fluide est incompressible (c’est le cas des liquides) alors la masse volumique est constante (elle reste la même en tout point du fluide)
Voir fiche de cours sur la masse volumique https://webphysique.fr/masse-volumique/
Lorsque le fluide est de l’eau douce alors sa masse volumique est proche de ρ = 1000 kg.m-3
Lorsqu’il s’agit d’eau de mer (eau salée) la masse volumique varie le plus souvent entre 1025 et 1050 kg.m-3
Voir fiche de cours sur la masse volumique de l’eau
Loi de Mariotte
Cette loi est aussi parfois appelée loi de Boyle-Mariotte.
La loi de Mariotte concerne les gaz, elles permet de prévoir l’évolution de leur volume à partir de leur pression et inversement.
Loi de Mariotte:
Si un gaz évolue d’un état n°1 ( de pression P1 et volume V1) vers un état n°2 (de pression P2 et volume V2) alors:
P1 x V1 = P2 x V2
où:
- Les deux volumes (V1 et V2) sont exprimés dans la même unité (tous les deux en mètre cube, tous les deux en litre….)
- Les deux pressions (P1 et P2) sont exprimées dans la même unité (en général en pascal)
Attention, cette relation est valable à condition que:
- la température du gaz ne change pas (pas d’échauffement ni de refroidissement)
- que la quantité de matière du gaz ne change pas (pas de gaz en plus ou de gaz en moins)
La loi de Mariotte permet de déterminer le volume que possède un gaz:
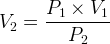
La loi de Mariotte permet aussi de déterminer la pression que possède un gaz:
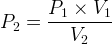
Voir:
Cours – La loi de Mariotte
Forces pressantes
Définition
Les forces pressantes sont les forces de poussée exercées par un fluide sur tout corps avec lequel ce fluide est en contact.
Caractéristiques
- Direction: perpendiculaire à la surface de contact entre le fluide et le corps.
- Sens: c’est une force de poussée qui s’exerce donc toujours du fluide vers le corps.
- Point d’application: les forces pressantes s’exercent en tous les points de la surface de contact, si la pression est uniforme (a même valeur sur toute la surface de contact) alors la résultante des forces pressantes a pour point d’application le centre de la surface de contact. (si par exemple la surface de contact est un carré alors le point d’application est le centre de ce carré)
- Valeur: elle peut être calculée grâce à la relation F = P x S (voir paragraphe suivant)
Valeur des forces pressantes
La valeur d’une force pressante peut être calculée grâce à la relation suivante:
F = P x S
où:
- F est la valeur de la force pressante en Newton (N)
- P est la pression exercée par le fluide au niveau de la surface de contact en Pascal (Pa)
- S est la valeur de la surface de contact en mètre carré (m2)
Cette relation indique que:
- La valeur de la force pressante est proportionnelle à la pression
- La valeur de la force pressante est proportionnelle à la surface de contact
Voir cours “Les forces pressantes” https://webphysique.fr/force-pressante/
Inversement lorsque la valeur d’une force pressante exercée par un fluide sur un corps est connue il est possible d’en déduire la valeur de la pression:
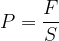
Voir cours Les forces pressantes
Loi fondamentale de la statique des fluides
Cette loi s’applique pour un un fluide au repos, c’est à dire sans mouvement (et donc sans écoulement) et incompressible (dont la masse volumique reste constante ou dont les variations sont assez faibles pour être négligées)
Elle résulte de l’application des lois de la mécanique à un système en équilibre pour lequel la somme des forces (forces pressantes et poids) est nulle.
La loi fondamentale de la statique des fluides s’exprime en considérant deux points distincts d’un même fluide:
Les altitudes ( z1 et z2 ) sont exprimées par rapport à une origine que l’on peut choisir librement: il s’agit souvent de la surface du fluide et parfois du fond d’un récipient.
Par contre l’axe des altitudes est toujours orienté vers le haut ce qui implique que si l’origine est choisi au niveau de la surface d’un fluide tout point sous cette surface possède une altitude “z” négative.

La loi fondentale de la statique des fluides s’exprime par la relation suivante:
P1 + ρgz1 = P2 + ρgz2
ou encore:
P1 – P2 = + ρg(z2 -z1)
où:
- P1 et P2 sont en pascal (Pa)
- ρ est la masse volumique du fluide auxquels appartiennent les point 1 et 2 en kilogramme par mètre cube (kg.m-3)
- Z1 et Z2 sont en mètre (m)
Cette expression peut être utilisée pour trouver:
- la pression au point n°1: P1 = P2 + ρgz2 – ρgz1 ou encore P1 = P2 + ρg(z2 – z1)
- la pression au point n°2: P2 = P1 + ρgz1 – ρgz2 ou encore P2 = P1 + ρg(z1 – z2)
- la différence de pression entre deux points: ΔP = P2 – P1 = ρg(z1 – z2)
- L’altitude z1:
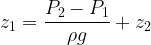
Interprétation de la relation fondamentale de l’hydrostatique:
- La pression augmente lorsque l’altitude diminue (plus un point est situé à une profondeur importante sous la surface et plus la pression y est élevée)
- La pression dépend de la masse volumique du fluide, celle-ci varie de manière plus importante avec l’altitude lorsque la masse volumique est plus élevée.
A réviser
Cours de seconde:
Les autres cours de première spécialité
- Quantité de matière, masse molaire et concentration
- Réaction d’oxydoréduction et avancement
- Titrage colorimétrique redox
- Schéma de Lewis, géométrie, électronégativité et polarisation
- Cohésion des solides, dissolution, solubilité, hydrophilie et lipophilie
- Structure et nomenclature des espèces organiques
- Synthèses d’espèces organiques
- L’énergie de la matière organique
- Interactions, champs électrostatiques et gravitationnels
Pour approfondir et découvrir
- Biographie de Blaise Pascal – Wikipedia
