Vision et image

Cours de physique niveau seconde – Ondes et signaux – Vision et image

• Propagation de la lumière dans le vide
• Propagation de la lumière dans la matière
• Vitesse de propagation de la lumière dans le vide
• Vitesse de propagation de la lumière dans l’air
• Vitesse de propagation de la lumière dans la matière
• Vitesse, durée et distance
• Indice de réfraction
• Longueur d’onde d’une lumière colorée
• Emission de lumière par la matière
• Qu’est-ce qu’un spectre ?
• Spectre continu
• Spectre de raies
• Propagation de la lumière lors d’un changement de milieu
• Elements et vocabulaire utilisés pour décrire la réflexion et la réfraction
• Trouver l’angle d’incidence
• La réflexion et ses lois
• La réfraction et ses lois
• Déterminer un angle de réfraction
• Prévoir le sens de déviation d’un rayon lors d’une réfraction
• Utiliser la loi de la réfraction de Snell-Descartes pour déterminer un indice de réfraction
• Dispersion de la lumière par un prisme
• Les lentilles
• Reconnaître une lentille convergente
• Reconnaître une lentille divergente
• Caractéristiques d’une lentille convergente
• Rayons particuliers pour une lentille convergente
• Image d’un point par une lentille convergente
• Image d’un objet plan par une lentille convergente
• Image réelle
• Le grandissement
• Modélisation d’un oeil

Propagation de la lumière dans le vide

Dans le vide la lumière se propage toujours en ligne droite, on peut ainsi la modéliser par un ou plusieurs rayons lumineux.

La lumière se propage en ligne droite dans le vide.

Un rayon lumineux est une droite (indiquant la direction de propagation de la lumière) munie d’une flèche (précisant le sens de propagation)

En général une source de lumière ne produit pas seulement un rayon lumineux mais un ensemble de rayons lumineux qui constituent un faisceau. Ce faisceau lumineux est en général modélisé par les deux rayons lumineux extrêmes qui le délimitent.

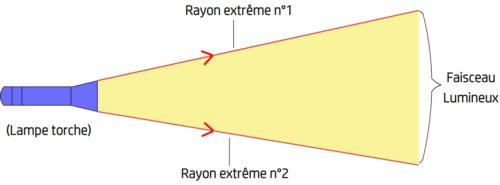
La lumière émise par une source peut être modélisée par des rayons lumineux qui peuvent constituer un faisceau lumineux.

Remarque

En classe de seconde, pour simplifier, on choisit souvent de se limiter à l’étude de rayons lumineux plutôt que de faisceaux lumineux.

Propagation de la lumière dans la matière

La lumière peut également se propager dans des milieux matériels dits “transparents”

Si une matière est transparente la lumière peut s’y propager

Dans une matière qui est chimiquement et physiquement homogène la lumière se propage aussi en ligne droite.

Une matière est physiquement et chimiquement homogène si:

• Sa composition chimique est la même en tous points.
• Dans l’ensemble de cette matière les grandeurs physiques restent constantes, c’est à dire qu’il n’y pas de variations de température, de pression, de densité au sein de cette matière.

Si une matière transparente est homogène alors la lumière s’y propage en ligne droite.

Vitesse de propagation de la lumière dans le vide

La vitesse de propagation de la lumière est aussi appelée célérité, on la note en général “c”

Dans le vide la lumière se propage à la vitesse la plus élevée possible: rien (aucun rayonnement, objet où particule) ne peut aller plus vite.

La valeur de cette vitesse de propagation doit être connue en classe de seconde, elle est de c = 3,00.10⁸ m.s^-1.

La lumière se propage dans le vide à une vitesse c = 3,00.10⁸ m.s^-1

En kilomètre par seconde cette vitesse est de c = 3,00.10⁵ km.s^-1.

Vitesse de propagation de la lumière dans l’air

Dans l’air la vitesse de propagation de la lumière est si peu différente de celle qu’elle possède dans le vide qu’on peut faire l’approximation qu’elle reste de 3,00.10⁸ m.s^-1.

Dans l’air la vitesse de propagation de la lumière est v = 3,00.10⁸ m.s^-1

Vitesse de propagation de la lumière dans la matière

Dans un milieu matériel transparent (solide, liquide ou gazeux) la vitesse de propagation de la lumière est toujours inférieure à celle qu’elle a dans le vide.

Il est possible d’exprimer la vitesse de propagation v_milieu de la lumière dans un milieu matériel par la relation:

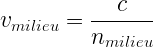
où:

• v_milieu est la vitesse de propagation de la lumière dans le milieu matériel ( en mètre par seconde)
• n_milieu est l’indice de réfraction de la lumière dans le milieu (sans unité)
• c est la vitesse de propagation de la lumière dans le vide (c = 3,00.10⁸ m.s^-1)

Par exemple l’eau douce a un indice de réfraction n_eau = 1,33

Donc:

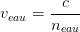
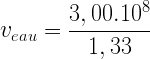
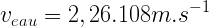
La vitesse de propagation de la lumière dans l’eau douce est donc de 2,26.10⁸ mètre par seconde.

Vitesse, durée et distance

Comme toute vitesse, la vitesse de propagation permet d’établir une relation entre une distance et une durée.

Cette vitesse de propagation peut être exprimée grâce à la relation suivante:

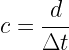
ou dans un milieu matériel:

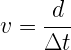
Il est possible d’’exploiter cette relation pour exprimer soit la distance parcourue soit la durée de propagation de la lumière .

La distance sur laquelle la lumière s’est propagée est donnée par la relation:

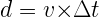
La durée de propagation de la lumière est donnée par la relation:

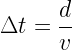
Indice de réfraction

L’indice de réfraction est une grandeur qui se note “n” et qui n’a pas d’unité. Tout milieu transparent possède un indice de réfraction qui le caractérise.

L’indice de réfraction d’un milieu est défini comme le rapport de la vitesse de la lumière dans ce milieu par la célérité de la lumière dans le vide.

Il peut être exprimé par la formule suivante:

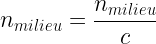
Il n’a pas d’unité car il est défini comme le rapport de deux grandeurs de même unité: pour obtenir l’indice de réfraction on divise des mètres par seconde par des mètres par seconde, il ne reste donc pas d’unités!

Puisque la vitesse de propagation de la lumière dans le vide est supérieure à celle de tout milieu matériel le rapport des deux est toujours supérieur à 1 et l’indice de réfraction est lui aussi toujours supérieur à 1 ( si vous trouvez un indice de réfraction inférieur à 1 dans un exercice c’est qu’il y a nécesssairement une erreur!)

L’indice de réfraction d’un milieu est une grandeur qui peut varier en fonction de différentes grandeurs telles que la température et la longueur d’onde de la lumière.

L’indice de réfraction joue un rôle dans dans le phénomène de réfraction (voir paragraphe sur la réfraction).

Remarque

L’indice de réfraction peut être exprimé avec la loi de la réfraction de Snell-Descartes. (voir paragraphe “Déterminer l’indice de réfraction à partir de la loi de la réfraction de Snell-Descartes”)

L’indice de réfraction:

• se note”n”
• n’a pas d’unité
• s’exprime à l’aide de la formule
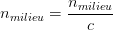
• est toujours supérieur à 1
• Varie en fonction de la température et de la longueur d’onde

Voir aussi cours “Indice de réfraction d’un milieu transparent“

Longueur d’onde d’une lumière colorée

Chaque lumière colorée est caractérisée par une longueur d’onde qui lui est propre.

La longueur d’onde se note avec la lettre λ (lettre grecque lambda) et s’exprime (comme toutes les longueurs) en mètre (m). On utilise cependant souvent des sous-unités et en particulier le nanomètre (nm). Pour rappel 1 nm = 10^-9 m et 1 m = 10⁹nm

Chaque lumière colorée possède une longueur d’onde notée λ (lambda) dont l’unité est le mètre (m) et qui s’exprime aussi souvent en nanomètre

Les lumières colorées possèdent une longueur d’onde qui va d’environ 400 nm à 800 nm:

Les lumières violettes ont des longueurs d’Ondes proches de 400 nm tandis que les lumières rouges ont des longueurs d’onde proches de 800 nm.

Entre ces deux valeurs extrêmes on trouve toutes les couleurs de l’arc-en-ciel (et dans le même ordre): après le violet il y a le bleu puis le vert, le jaune, l’orange et le rouge avec toutes les nuances possibles.

Les lumières colorées ont des longueurs d’onde comprises entre 400 nm (lumières violettes) et 800 nm (lumières rouges)

Si une lumière colorée n’est caractérisée que par une seule longueur d’onde alors il s’agit d’une lumière monochromatique (c’est en quelques sortes une lumière “pure”).

Si une lumière est caractérisée par plusieurs longueurs d’onde (voire par un intervalle de longueurs d’onde) alors il s’agit d’une lumière polychromatique où sont combinées plusieurs lumières colorées.

Une lumière est monochromatique si elle caractérisée par une seule longueur d’onde mais elle est dite polychromatique si elle est caractérisée par plusieurs longueurs d’onde.

Voir aussi cours “La longueur d’onde“

Emission de lumière par la matière

Il existe deux mécanismes qui permettent à la matière d’émettre de la lumière.

• Le premier est l’incandescence: toute matière atteignant une température assez élevée finit par émettre une lumière polychromatique dont la couleur dominante varie avec la température. Les températures les plus basses sont associées à une lumière rougeâtre tandis que les corps incandescents les plus chaud émettent des couleurs bleutées voire violettes.

• Le deuxième mécanisme est l’excitation: lorsque la matière reçoit de l’énergie, les électrons initialement situés dans les couches électroniques basses “sautent” vers des couches plus élevées d’énergie plus grande. Cet état dit “excité” n’est pas stable et ces électrons finissent par “redescendre” vers des couches électroniques plus basses en libérant de l’énergie sous forme de lumière.

La matière peut émettre de la lumière par incandescence ou sous l’effet d’une excitation

Qu’est-ce qu’un spectre ?

Toute lumière possède un spectre qui présente l’ensemble des lumières monochromatiques la constituant. Il peut prendre la forme d’une figure (ou d’une photo) où les différentes lumières colorées sont sous forme de raies colorées mais il peut aussi s’agir d’une énumération des longueurs d’onde des différentes lumières monochromatiques.

Le spectre d’une lumière correspond à l’ensemble des différentes lumières monochromatiques qui constituent cette lumière.

Le spectre d’une lumière peut être visualisé grâce à un appareil appelé spectroscope qui comprend un élément dit “dispersif” (comme un prisme ou un réseau). Cet élément dispersif permet de dévier les lumières d’un angle qui dépend de leur longueur d’onde.

Un spectroscope (à base d’un spectre ou d’un prisme) permet d’obtenir le spectre d’une lumière

Spectre continu

Le spectre d’une lumière est dit continu s’il couvre un intervalle complet (continu !) de longueurs d’onde. Une lumière ayant un spectre continu a toujours une origine thermique, elle est toujours émise par un corps incandescent. Par exemple, la lumière émise par la surface du Soleil possède un spectre continu, c’est aussi le cas de la lave incandescente d’un volcan.

Remarques

Les lumières constituant un spectre continu n’ont pas nécessairement toutes la même intensité.

Un spectre continu obtenu à l’aide d’un spectroscope se présente sous la forme d’un dégradé de couleurs.

Exemple de spectre continu

La lumière d’une source incandescente possède un spectre continu qui comprend un intervalle complet de longueurs d’onde.

Voir aussi cours “Les spectres d’émission et d’absorption“

Spectre de raies

Si une source émet de la lumière par excitation (électrique par exemple) alors cette lumière possède un spectre de raies. Ce spectre est caractérisé par un nombre limité de longueurs d’onde ( cela peut aller d’une seule à une dizaine) qui forment chacune une raie colorée.

Un spectre de raies est composé d’un nombre limité de raies colorées chacune caractérisée par sa longueur d’onde.

Exemple

Propagation de la lumière lors d’un changement de milieu

Lorsque la lumière arrive à la surface qui sépare deux milieux transparents (par exemple l’air et l’eau ou le verre et un plastique) alors il peut se produire deux phénomènes différents: la réflexion et la réfraction.

Il est possible qu’il se produise seulement une réflexion ou seulement une réfraction ou encore que les deux phénomènes se produisent en même temps en des proportions variables.

Lorsqu’une lumière arrive au niveau de la surface de séparation de deux milieux transparents elle peut être réfléchie ou réfractée.

Voir aussi cours “La réfraction“

Elements et vocabulaire utilisés pour décrire la réflexion et la réfraction

L’étude de la réfraction et de la réflexion ainsi que l’expression des lois associées à ces phénomènes nécessitent de définir à un certains nombre de termes.

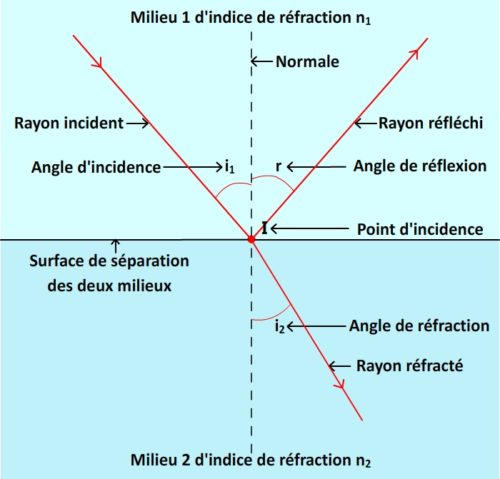
Tous d’abord les rayons:

• Celui qui se propage en direction de la surface de séparation des deux milieux transparent est appelé rayon incident.
• S’il y a réflexion alors le rayon “renvoyé” dans son milieu d’origine est appelé rayon réfléchi
• S’il y a réfraction alors le rayon lumineux passant dans le nouveau milieu transparent est appelé rayon réfracté

Un point:

• Le point de la surface de séparation des deux milieux transparents atteint par le rayon incident est appelé point d’incidence, il est souvent noté “I”.

Une droite:

• La droite perpendiculaire à la surface de séparation des milieux qui passe par le point d’incidence est appelée “normale”

Des angles:

• l’angle formé par la normale et le rayon incident est appelé angle d’incidence, on le note en général “i₁”.
• l’angle formé par la normale et le rayon réfléchi (s’il y a réflexion) est appelé angle de réflexion il souvent noté “r” .
• l’angle formé par la normale et le rayon réfracté (s’il y a réfraction) est appelé angle de réfraction. Il est souvent noté “i₂”

Des indices de réfraction:

• L’indice de réfraction du premier milieu (celui du rayon incident) est noté n₁
• L’indice de réfraction du deuxième milieu (celui du rayon réfracté) est noté n₂

Trouver l’angle d’incidence

L’angle d’incidence correspond à l’angle entre le rayon incident et la normale il peut:

• être indiqué par l’énoncé de l’exercice
• être mesuré sur une figure au rapporteur
• être déterminé à partir de l’angle entre le rayon incident et la surface de séparation

Si l’on connait l’angle α entre le rayon incident et la surface de séparation des milieux alors on peut en déduire l’angle d’incidence i₁ :

L’angle entre la normale et la surface de séparation des milieux est toujours, par définition, de 90° par conséquent la somme de l’angle d’incidence et de α vaut 90 ° soit i₁ + α = 90°, on en déduit donc que i₁ = 90° – α

Si l’angle entre le rayon incident et la surface de séparation a une valeur α alors la valeur de l’angle d’incidence est: i₁ = 90° – α

La réflexion et ses lois

Définition

Lorsqu’un rayon lumineux atteint la surface qui sépare son milieu de propagation d’un autre milieu transparent alors on dit qu’il y a réflexion si la lumière est déviée mais ne change pas de milieu.

Un rayon lumineux est réfléchi s’il est renvoyé dans son milieu de propagation d’origine.

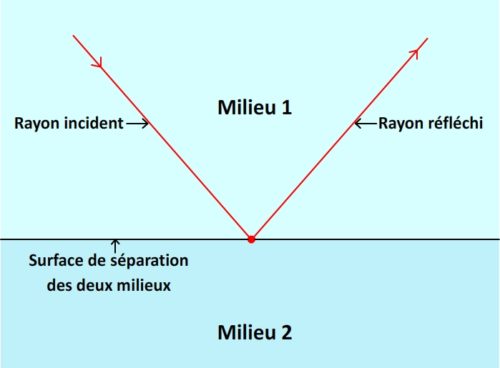
La réflexion est décrite par une loi appelée loi de la réflexion de Snell-Descartes.

Cette loi affirme d’une part que le rayon réfléchi reste dans le même plan que le rayon incident et la normale, d’autre part elle affirme que l’angle de réfraction a même valeur que l’angle d’incidence: i₁ = r

Loi de la réflexion de Snell-Descartes:

le rayon réfléchi appartient au plan formé par le rayon incident et la normale

i₁ = r

La réfraction et ses lois

Définition

Il y a réfraction de la lumière lorsque cette dernière franchit la surface séparation de deux milieux transparents et subit alors une déviation (c’est à dire que la direction de propagation change).

Il y a réfraction lorsque la lumière est déviée lors de la transition d’un milieu transparent vers un autre.

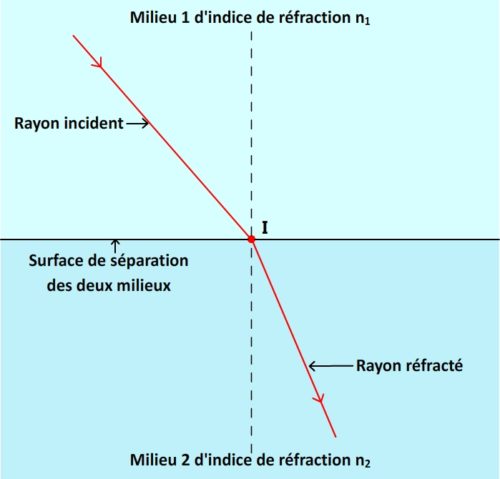
La réfraction se produit lorsque l’angle d’incidence n’est pas nul et que la lumière passe vers un nouveau milieu transparent dont l’indice de réfraction est différent de celui du milieu initial.

Plus la différence d’indice de réfraction est importante entre les deux milieux et plus la réfraction conduit à une déviation importante.

La réfraction d’un rayon lumineux est décrite par la loi de Snell-Descartes de la réfraction qui affirme que le rayon réfracté, le rayon incident et la normale sont tous dans le même plan et qu’il existe entre l’angle d’incidence, l’angle de réfraction et les indices de réfraction la relation suivante: n₁ x sin (i₁) = n₂ x sin (i₂)

Loi de la réfraction de Snell-Descartes:

Le rayon réfracté est dans le même plan que la normale et le rayon incident

n₁ x sin (i₁) = n₂ x sin (i₂)

Voir aussi cours “Loi de Snell-Descartes de la réfraction“

Déterminer un angle de réfraction

Pour déterminer un angle de réfraction “i₂” on peut exploiter la loi de Snell-Descartes de la réfraction. Selon cette loi on a la relation suivante:

n₁ x sin (i₁) = n₂ x sin (i₂)

On peut isoler le sinus de l’angle de réfraction:

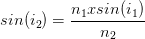
Lorsque cette valeur (sin (i₂)) a été calculée il faut utiliser la fonction réciproque du sinus que l’on trouve sur toute calculatrice scientifique. Cette fonction réciproque est appelée fonction “arcsinus”, elle en générale notée “Arcin” ou “sin^-1” sur la calculatrice.

Attention à bien vérifier que la calculatrice est réglée en “mode degré”

Pour déterminer un angle de réfraction:

on calcule d’abord le sinus de l’angle de réfraction avec la relation :

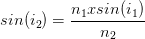
La valeur de l’angle de réfraction est obtenue grâce à la fonction réciproque du sinus (arcin ou sin^-1) de la calculatrice

Exemple

Un rayon lumineux se propage dans l’air (milieu d’indice de réfraction n₁ = 1 ) et pénètre dans l’eau (milieu d’indice de réfraction n₂ = 1,33) avec un angle d’incidence de 50°)

Le sinus de l’angle de réfraction a pour valeur:

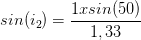
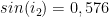
La fonction sinus réciproque de la calculatrice permet de trouver:

i2 = 35,2°

Prévoir le sens de déviation d’un rayon lors d’une réfraction

Le sens de la déviation qui se produit lors d’une réfraction dépend des indices de réfraction n₁ et n₂ des deux milieux:

Si les deux milieux on le même indice de réfraction (n₁ = n₂ ) alors il n’y a pas de déviation (et donc pas de réfraction!)

Si le deuxième milieu a un indice de réfraction plus élevé que le premier (n₁ < n₂ ) alors le rayon réfracté se rapproche de la normale

Si le deuxième milieu a un indice de réfraction plus faible que le premier (n₁ > n₂ ) alors le rayon réfracté s’éloigne de la normale

Utiliser la loi de la réfraction de Snell-Descartes pour déterminer un indice de réfraction

La loi de la réfraction de Snell-Descartes est une relation entre les angles (i₁ et i₂) et les indices de réfraction:

n₁ x sin (i₁) = n₂ x sin (i₂)

Cette relation permet d’exprimer n₁ ou n₂:

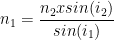
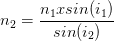
Exemple

Un rayon se propage dans l’air (milieu d’indice n₁ = 1) et pénètre dans un deuxième milieu (d’indice de réfraction n₂ inconnu) avec un angle d’incidence i1 = 64°. L’angle de réfraction est de i2 = 56°

Il est possible de déterminer l’indice de réfraction du deuxième milieu:

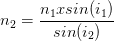
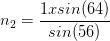
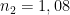
Dispersion de la lumière par un prisme

Le prisme est un solide droit à base triangle constitué d’un matériau dispersif caractérisé par un indice de réfraction très sensible à la longueur d’onde de la lumière (pour des lumières de longueurs d’onde différentes les indices de réfraction sont différents).

Un prisme fait subir une double réfraction à la lumière, la première au niveau de sa face d’entrée et la deuxième au niveau de sa face de sortie or l’angle de réfraction dépend de l’indice de réfraction:

Des lumières colorées de longueurs d’onde différentes subissent donc des réfractions d’angles différents.

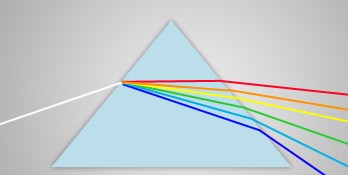
Un prisme dévie de manières différentes des lumières ayant des longueurs d’onde différentes, on dit que le prisme décompose ou disperse la lumière, il permet d’obtenir son spectre.

Remarque

Un réseau exploite un mécanisme différent mais permet également de décomposer la lumière.

Les lentilles

Définition

Une lentille est un milieu transparent limité par deux faces et qui présente une symétrie par rapport à un axe central.

Une lentille fait subir à la lumière deux réfractions successives, la première lorsqu’elle pénètre par la première face (transition air-milieu transparent de la lentille) et la seconde lors de la sortie de la lentille (transition milieu transparent de la lentille – air).

Ces deux réfractions successives permettent à la lentille de modifier le trajet de la lumière et de former des images des sources émettrices de lumière.

Il existe deux grandes familles de lentilles: les lentilles convergentes et les lentilles divergentes

Une lentille est un milieu transparent avec deux faces, un axe de symétrie.

Les réfractions qu’elle fait subir à la lumière permet de dévier celle-ci et de former des images.

Il existe des lentilles convergentes et des lentilles divergentes

Les lentilles convergentes et divergentes se distinguent par leur forme, leur symbole et l’effet qu’elles ont sur la lumière.

Reconnaitre une lentille convergente

On peut reconnaître une lentille convergente en l’examinant: elle est plus épaisse en son centre qu’au niveau de ses bords.

Les modèles les plus fréquents de lentilles convergentes sont bombés (elles présentent deux faces convexes) mais on peut aussi trouver des modèles avec une face convexe et une face plane, ou encore avec une face convexe et une face concave.

Son symbole est le suivant:

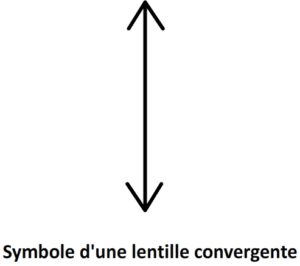
Si une lentille convergente reçoit un faisceau de lumière parallèle alors elle fait converger tous les rayons lumineux vers le même point. Si l’on éclaire une lentille convergente avec un faisceau lumineux parallèle, après cette lentille son diamètre diminue progressivement et fini par former un simple point lumineux.

Pour savoir si une lentille est convergente on peut aussi réaliser un test pratique simple qui consiste à déposer cette lentille sur une page de texte: si les caractères de ce texte apparaissent grossis alors cette lentille est bien convergente.

Une lentille convergente peut se reconnaitre:

en vérifiant que ses bords sont plus minces que son centre

à partir de son symbole

en vérifiant qu’elle fait converger un faisceau parallèle en un point

en vérifiant qu’elle grossit un texte sur lequel elle est posée.

Reconnaitre une lentille divergente

Il est possible de reconnaître une lentille divergente à partir de son aspect: elle présente toujours des bords plus épais que sont centre (c’est le contraire des lentilles convergentes).

Le plus souvent les lentilles divergentes possèdent deux faces concaves mais on peut aussi trouver des modèles avec une face concave et une face plane ou avec une face concave et une face convexe.

Son symbole est le suivant:

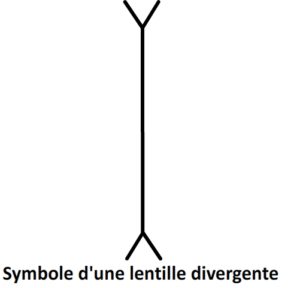
Une lentille divergente a pour effet de faire diverger un faisceau lumineux parallèle: les rayons lumineux initialement tous parallèles entre eux s’éloignent les uns des autres, on dit qu’ils divergent.

La tache lumineuse formée par un tel faisceau est de plus en large.

Pour identifier une lentille divergente on peut aussi se baser sur un test pratique simple: lorsqu’une lentille divergente est posée sur un texte celui-ci apparaît plus petit (les caractères sont rétrécis)

Une lentille divergente peut donc se reconnaître:

à ses bords plus épais que son centre

à son symbole

en vérifiant qu’elle fait diverger (élargit) un faisceau parallèle

en vérifiant qu’un texte sur lequel elle est posée apparaît plus petit

Caractéristiques d’une lentille convergente

Une lentille convergente est caractérisée par un ensemble d’éléments qui reflètent son degré de convergence et permettent de prévoir le chemin de la lumière.

L’axe optique

Par définition, toutes les lentilles disposent d’un axe de symétrie perpendiculaire aux faces d’entrée et de sortie, cet axe correspond à l’axe de symétrie de la lentille:

• il se note Δ
• il est orienté dans le sens de propagation de la lumière (le plus souvent de gauche à droite)
• il passe toujours par le centre de la lentille
• il peut être représenté en trait plein ou en pointillé (pour le différencier des rayons lumineux)
• une flèche précise son sens d’orientation

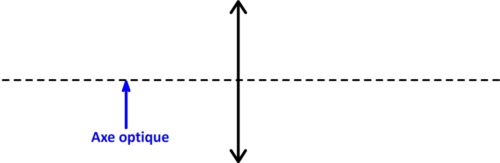
Toute lentille convergente possède un axe optique qui coïncide avec l’axe de symétrie de la lentille. il est noté Δ, orienté dans le sens de propagation de la lumière et passe par le centre de cette dernière.

Le centre optique

Il correspond au centre de la lentille:

• se note O
• c’est un point appartenant à la fois à l’axe optique et à la lentille

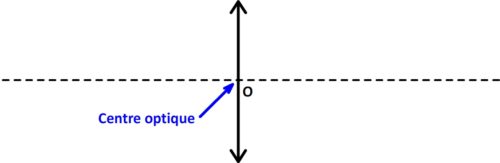
Le centre optique d’une lentille correspond à son centre géométrique, se note “O”, il appartient à la fois à l’axe optique et à la lentille.

Le foyer image

Il correspond au point de convergence de la lentille:

• il se note F’
• il est situé sur l’axe optique, à droite du centre optique
• il se trouve à une distance du centre optique appelée “distance focale”
• c’est le point où convergent des rayons lumineux qui sont parallèles à l’axe optique avant de rencontrer la lentille convergente.
• Plus le foyer image est proche du centre optique et plus la lentille est convergente.

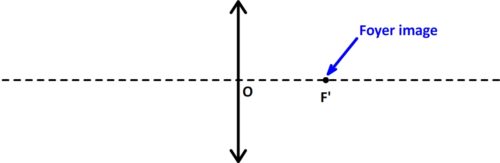
Le foyer image d’une lentille se note “ F’ “, il est situé sur l’axe optique, à droite du centre optique et des rayons lumineux parallèles à l’axe optique avant la lentille s’orientent tous vers ce point (on dit qu’ils “convergent”) après l’avoir traversée.

Le foyer objet

C’est le symétrique du foyer image par rapport au centre optique:

• il se note F
• il est situé sur l’axe optique, à gauche du centre optique
• la distance qui le sépare du centre optique correspond à la “distance focale”
• touts les rayons lumineux incidents qui passent par ce point émergent de la lentille parallèles à l’axe optique.
• Plus le foyer objet est proche du centre optique et plus la lentille est convergente.

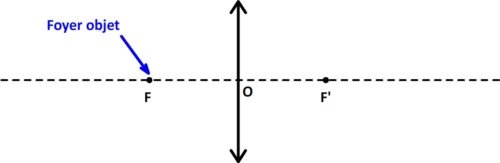
Le foyer objet est un point noté “F” situé sur l’axe optique, à gauche du centre optique et tous les rayons incidents qui y passent émmergent parallèles à l’axe optique.

La distance focale

Il s’agit de la distance séparant le centre optique et le foyer objet:

• Elle se note f’
• Elle correspond à la distance OF’ et à la distance FO
• Elle est d’autant plus faible que la lentille est convergente.

La distance focale d’une lentille convergente se note “ f’ “ et correspond à la distance entre le centre optique et l’un de ses foyers (objet ou image). Sa valeur est d’autant plus faible que la lentille est convergente.

Rayons particuliers pour une lentille convergente

Les rayons particuliers sont des rayons lumineux incidents dont il est facile de prévoir la direction, à la sortie de la lentille, à partir des caractéristiques de cette dernière (le centre optique, les foyers….).

On distingue trois rayons particuliers:

• Rayon incident passant par le centre optique

Tout rayon passant par le centre optique n’est pas dévié, il conserve la même direction.

Pour tracer le rayon qui émerge de la lentille il suffit de prolonger le rayon incident

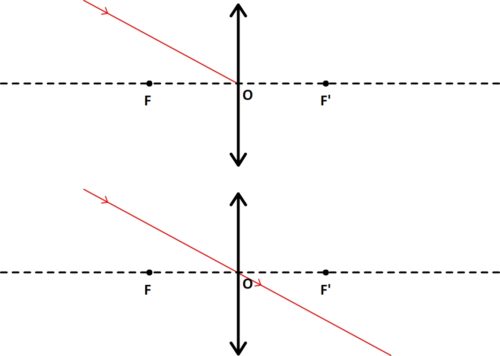
• Rayon incident parallèle à l’axe optique

Tout rayon incident parallèle à l’axe optique émerge de la lentille en se dirigeant vers le foyer image.

Dans ce cas, pour tracer le rayon émergent, il suffit de tracer la droite passant par le foyer image F’ et le point commun au rayon incident et à la lentille.

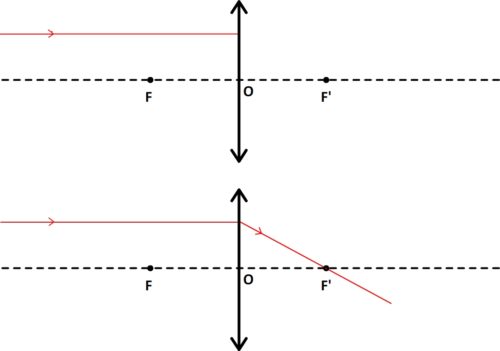
• Rayon incident passant par le foyer objet

Tout rayon incident passant par le foyer objet émerge de la lentille parallèle à l’axe optique.

Pour tracer le rayon émergeant il suffit de tracer la droite parallèle à l’axe optique débutant au point où le rayon incident “frappe” la lentille.

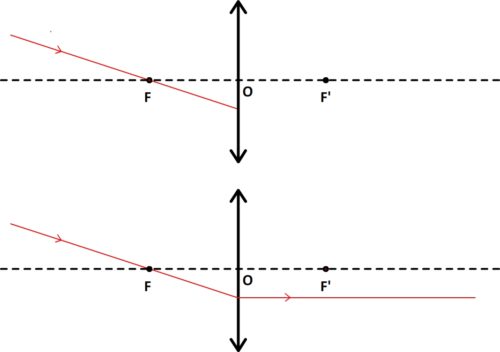
Image d’un point par une lentille convergente

Tout point d’un objet se comporte comme une source de lumière: soi une source primaire qui produit de la lumière (objet incandescent, phosphorescent…) soi une source secondaire qui diffuse la lumière (reçue du Soleil, d’une lampe, d’un autre objet…)

Chaque point d’un objet émet donc de la lumière dans toutes les directions et éclaire toute la surface d’une lentille divergente.

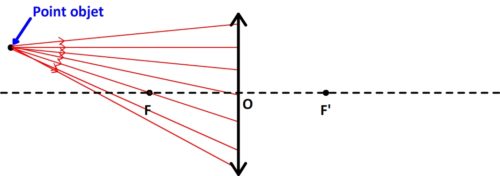
Après avoir traversé une lentille convergente, la lumière émise par un point converge en un autre point qui constitue l’image.

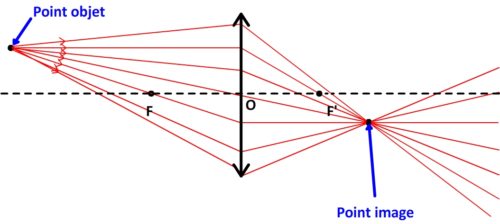
Ainsi:

• le point qui émet la lumière est appelé le point objet.
• le point de convergence est appelé point image.

Tout rayon lumineux issu d’un point objet converge après la lentille en point qui correspond au point image.

Pour trouver un point image il est inutile de tracer tous les rayons émis et déterminer tous les rayons émergents:

Pour trouver un point image il suffit de tracer deux rayons particuliers et de chercher le point d’intersection des deux rayons émergents.

Le plus souvent on trace le rayon incident qui passe par le centre optique et celui qui est parallèle à l’axe optique.

Le point image est noté avec la même lettre que le point objet mais suivi d’un “prime”:

• L’image d’un point A est notée A’
• L’image d’un point B est notée B’
• L’image d’un point C est notée C’

etc

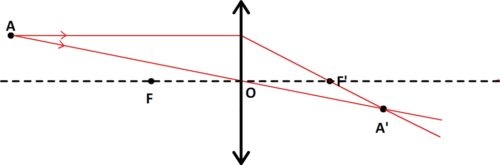
Image d’un objet plan par une lentille convergente

Un objet est un ensemble de points par conséquent, pour trouver l’image d’un objet il suffit de trouver les images des différents points qui constituent cet objet.

Le programme de seconde se limite aux cas d’objets plans, c’est à dire d’objet dont tous les points appartiennent à un même plan, qui sont en général perpendiculaire à l’axe optique.

La formation d’une image obéit à quelques règles simples:

• Si des points objets appartiennent au même plan alors leurs images appartiennent aussi au même plan.
• Si des points objets appartiennent au même segment alors leurs images appartiennent aussi au même segment.

Par conséquent, pour trouver l’image d’un segment par une lentille il suffit de trouver l’image des deux points objets qui limitent ce segment objet:

L’image d’un segment AB par une lentille convergente est un segment A’B’

Pour trouver l’image d’un segment AB par une lentille convergente il suffit donc:

• de déterminer le point image A’ en traçant des rayons particuliers issus du point objet A
• de trouver le point image B’ en traçant des rayons particuliers issus du point objet B
• de tracer le segment A’B’ qui constitue l’image du segment AB

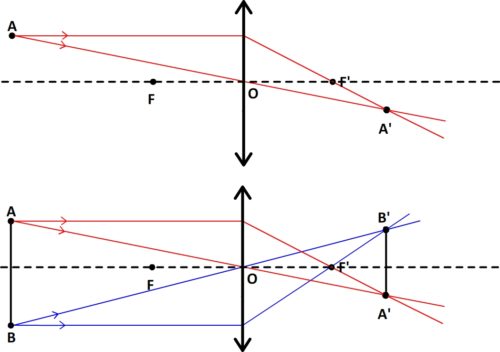
Souvent, en seconde, les objets étudiés sont des segments:

• perpendiculaires à l’axe optique.
• qui ont une extrémité appartenant à l’axe optique.

Dans ce cas, pour obtenir l’image d’un objet AB où le point B appartient à l’axe optique il suffit:

• de trouver la position du point image A’ en traçant des rayons particuliers
• de placer le point image B’ sur l’axe optique à la verticale du point A’
• de joindre le point A’ au point B’ pour obtenir le segment A’B’ qui constitue l’image du segment AB

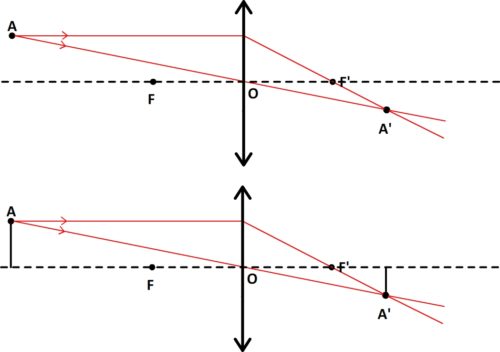
Image réelle

Définition

L’image d’un objet est dite réelle si elle peut se former sur un écran.

Une lentille convergente ne forme une image réelle que si l’objet est situé avant le foyer objet.

Le grandissement

Le grandissement est une grandeur:

• souvent notée avec la lettre grecque γ (gamma)
• qui n’a pas d’unité
• dont la valeur correspond au rapport de la dimension de l’image par celle de l’objet

Si l’objet est un segment AB d’image A’B’ alors le grandissement peut être exprimé par la relation:

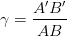
Le grandissement permet de comparer la taille de l’image et celle de l’objet:

• Si le grandissement est supérieur à 1 (γ > 1) alors il y a un agrandissement: l’image est plus grande que l’objet
• Si le grandissement est inférieur à 1 (γ < 1) alors il y a un rétrécissement: l’image est plus petite que l’objet
• Si le grandissement est égal à 1 (γ = 1) alors la taille de l’image est égale à celle de l’objet.

Exemples:

• Si γ = 3 alors l’image est trois fois plus grande que l’objet.
• Si γ = 0,5 alors l’image est deux fois plus petite que l’objet

Le grandissement est une grandeur notée γ (gamma) sans unité correspondant au rapport de la taille de l’image par la taille de l’objet. Il est supérieur à “1” lorsque l’image est plus grande que l’objet mais il est inférieur à “1” si l’image est plus petite.

Modélisation d’un oeil

L’humain est un système biologique complexe néanmoins il est possible de modéliser son action sur la lumière de manière assez simple.

L’oeil humain est comparable à l’association:

• d’une lentille convergente (qui joue le même rôle que le cristallin)
• d’un écran (qui joue le même rôle que la rétine)

L’oeil humain peut être modélisé comme l’association d’une lentille convergente et d’un écran.

Les autres cours de physique-chimie niveau seconde

• Corps purs et mélanges au quotidien
• Les solutions aqueuses, un exemple de mélange
• Du macroscopique au microscopique, de l’espèce chimique à l’entité
• Le noyau de l’atome, siège de sa masse et de son identité
• Le cortège électronique de l’atome définit ses propriétés chimiques
• Vers des entités plus stables chimiquement
• Transformation physique
• Transformation chimique
• Transformation nucléaire
• Décrire un mouvement
• Modéliser une action sur un système
• Principe d’inertie
• Emission et perception d’un son
• Vision et image
• Circuits électriques
• Capteurs