L’énergie de la matière organique

Cours de physique-chimie | première spécialité

Ce cours correspond à la partie “C) Conversion de l’énergie stockée dans la matière organique” du programme de première spécialité.

Il est situé dans la partie du programme “Constitution et transformations de la matière – Propriétés physico-chimiques, synthèses et combustions d’espèces chimiques organiques”

Combustion de la matière organique

• Rappels sur les combustions
• Les combustibles organiques
• Combustion et oxydoréduction
• Exemple: combustion du méthane
• Combustion des alcanes
• Combustion des alcools

Les énergies de liaison

• Energie de liaison
• Energie de liaison d’une molécule
• Calcul de l’énergie molaire de liaison de la molécule de méthane
• Calcul de l’énergie molaire de liaison de la molécule de propane
• Calcul de l’énergie molaire de liaison de la molécule de l’éthanol

Energies de réaction

• Définition de l’énergie molaire de réaction
• Méthode n°1 pour calculer l’énergie molaire de réaction
• Méthode n°2 pour calculer l’énergie molaire de réaction
• Exemple – Calcul de l’énergie molaire de réaction pour la combustion du propane
• Exemple – Calcul de l’énergie molaire de réaction pour la combustion de l’éthanol
• Energie de réaction
• Pouvoir calorifique massique
• Calculer le pouvoir calorifique massique

REVISER – AUTRES COURS DE PREMIERE SPECIALITE – APPROFONDIR ET DECOUVRIR

Combustion de la matière organique

Rappels sur les combustions

Une combustion est une transformation chimique dont l’un des réactifs est un combustible et l’autre est un comburant.

Le combustible est une substance capable de brûler qui peut être solide, liquide ou gazeuse.

Exemples de combustibles: l’éthanol, le dihydrogène, l’huile, le méthane, le papier, la laine de fer….

Remarque: un combustible qui alimente un moteur à combustion est appelé “carburant“. Ainsi l’éthanol, l’essence, l’huile végétale, le kérozène sont des combustibles utilisables comme carburant.

Le comburant est une substance capable de réagir avec le combustible.

Dans la majorité des cas le comburant est du dioxygène O₂.

Une combustion débute toujours par une phase d’amorçage au cours de laquelle une quantité suffisante d’énergie (l’énergie d’activation) est reçue par le combustible (fournie par la flamme d’une autre combustion, par une étincelle, un frottement ou encore un rayonnement…)

Les combustions sont des transformations exothermiques (voir cours sur les transformations exothermiques et endothermique)

La quantité de chaleur libérée par une combustion est si élevée qu’elle conduit la formation d’une flamme, à l’incandescence du combustible solide ou à une explosion)

Les combustibles organiques

Définition

Un combustible organique est une substance capable de subir une combustion composée d’espèces chimiques de nature organique (voir cours sur les espèces chimiques organiques )

Toute les espèces chimiques organiques peuvent jouer le rôle de combustible

La combustion d’une espèce organique avec le dioxygène produit toujours au moins de l’eau (H₂O) et du dioxyde de carbone (CO₂)

Le dioxyde de carbone se forme par combinaison des carbones de l’espèce organique et de l’oxygène présent dans le dioxygène.

L’eau se forme par combinaison des atomes d’hydrogène de l’espèce organique et de l’oxygène du dioxygène.

Les combustibles organiques peuvent être d’origine fossile (c’est principalement le cas des alcanes), ils sont alors issus de ressources formées par des processus lents qui ne permettent pas leur renouvellement à l’échelle d’une (et même plusieurs !) vie humaine. Les principaux combustibles organiques fossiles sont les constituant du pétrole du gaz naturel.

Les combustibles organiques peuvent aussi être issus de la biomasse comme le bioéthanol, le biogaz, ou plus simplement le bois. Leur combustion a l’avantage de ne pas augmenter le taux de CO₂ dans l’air (et de ne pas contribuer à augmenter l’effet de serre et les températures) car le dioxyde de carbone produit par leur combustion ne fait que rendre à l’atmosphère le dioxyde de carbone qui avait été consommé par la photosynthèse (les plantes produisent grâce à la photosynthèse les matières organiques à l’origine de toutes les chaînes alimentaires).

Combustion et oxydoréduction

Une combustion est une réaction d’oxydoréduction entre:

• un combustible qui est toujours un réducteur
• un comburant (en général le dioxygène) qui est toujours un oxydant

Lors d’une combustion:

• l’espèce organique fait partie d’un couple oxydant-réducteur du type CO₂/espèceorganique
• le dioxygène fait partie du couple oxydant-réducteur O₂/H₂O

Exemple de la combustion du méthane (CH₄)

On peut considérer que la combustion du méthane avec le dioxygène est la réaction entre:

• le méthane du couple CO₂/CH₄
• le dioxygène du couple O₂/H₂O

La demi-équation d’oxydation du méthane est:

CH₄ + 2H₂O → CO₂ +8H⁺ +8e^–

La demi-équation de réduction du dioxygène est:

O₂ +4H⁺ +4e^– → 2H₂O

La combinaison des deux demi-équations permet d’obtenir l’équation d’oxydoréduction complète:

CH₄ + 2H₂O → CO₂ +8H⁺ +8e^–

+ O₂ +4H⁺ +4e^– → 2H₂O X2

_________________________________________________

CH₄ + 2H₂O + 2O₂ +8H⁺ +8e^– → CO₂ +8H⁺ +8e^– + 4H₂O

Cette équation peut être simplifiée en supprimant “8e^– “, “8H⁺” et en retirant “2H₂O” de chaque coté. On obtient alors:

CH₄ + 2O₂ → CO₂ + 2H₂O

Combustion des alcanes

La combustion d’un alcane avec le dioxygène ne forme que de l’eau et du dioxygène.

Les équations de réaction peuvent être équilibrées en passant par l’intermédiaire des demi-équations d’oxydoréduction mais il est aussi possible de les écrire et de les équilibrer directement.

Exemples

• Equation de réaction de combustion du méthane:

CH₄ + 2O₂ → CO₂ + 2H₂O

• Equation de réaction de combustion de l’éthane:

2C₂H₆+ 7O₂ → 4CO₂ + 6H₂O

• Equation de réaction de combustion du propane

C₃H₈+ 5O₂ → 3CO₂ + 4H₂O

• Equation de réaction de combustion du butane

2C₄H₁₀+ 13O₂ → 8CO₂ + 10H₂O

• Equation de réaction de combustion du pentane

C₅H₁₂+ 8 O₂ → 5CO₂ + 6H₂O

D’une manière général pour un alcane de formule générale C_nH_2n+2:

• si n est impair alors l’équation de réaction est de la forme

C_nH_2n+2+ (3n+1/2)O₂ → nCO₂ + (n+1)H₂O

• si n est pair alors l’équation de réaction est de la forme

2C_nH_2n+2 + (3n+1)O₂ → 2nCO₂ + 2(n+1)H₂O

Combustion des alcools

La combustion d’un alcool ne forme également que de l’eau et du dioxyde de carbone.

• Equation de réaction de combustion du méthanol:

2CH₄O+ 3O₂ → 2CO₂ + 4H₂O

• Equation de réaction de combustion de l’éthanol:

C₂H₆O+ 3O₂ → 2CO₂ + 3H₂O

• Equation de réaction de combustion du propanol

2C₃H₈O+ 9O₂ → 6CO₂ + 8H₂O

• Equation de réaction de combustion du butanol

C₄H₁₀O+ 6O₂ → 4CO₂ + 5H₂O

• Equation de réaction de combustion du pentanol

2C₅H₁₂O + 15O₂ → 10CO₂ + 12H₂O

D’une manière général pour un alcool de formule générale C_nH_2n+2O:

• si n est pair alors l’équation de réaction est de la forme

C_nH_2n+2O+ (3n/2)O₂ → nCO₂ + (n+1)H₂O

• si n est impair alors l’équation de réaction est de la forme

2C_nH_2n+2O+ 3n O₂ → 2nCO₂ + 2(n+1)H₂O

---

Les énergies de liaison

Energie de liaison

Lorsque deux atomes “A” et “B” sont liés par une liaison covalente A-B alors l’énergie de la liaison A-B correspond à l’énergie minimale qui permet de séparer ces deux atomes et ainsi rompre leur liaison.

L’énergie de liaison est en général exprimée sous forme d’énergie de liaison molaire:

Définition

L’énergie molaire de liaison entre deux atomes correspond à l’énergie nécessaire pour rompre une mole de liaisons entre ces deux atomes.

Pour une un liaison entre un atome A et un atome B elle est notée El(A-B) ou El_A-B

Elle s’exprime en kilojoule par mole (kJ.mol^-1)

Elle est toujours positive: la rupture d’une liaison est une transformation endothermique qui consomme de l’énergie.

Exemples d’énergies molaires de liaison

• Energie molaire de liaison carbone-hydrogène: El(C-H) = 413 kJ.mol^-1
• Energie molaire de liaison carbone-carbone: El(C-C) = 346 kJ.mol^-1

Energie molaire de liaison d’une molécule

Définition

L’énergie molaire de liaison d’une molécule (aussi appelée énergie molaire de liaison moléculaire) correspond à l’énergie qu’il faudrait pour rompre une mole de chacune des liaisons de cette molécule.

Elle se note en générale El(nom de la molécule) et s’exprime en kilojoule par mole (kJ.mol^-1)

Par exemple l’énergie molaire de liaison de la molécule de méthane est:

El(méthane) = 1652 kJ.mol^-1

Pour calculer l’énergie molaire de liaison d’une molécule il suffit d’ajouter l’énergie molaire de chacune de ses liaisons.

Calcul de l’énergie molaire de liaison de la molécule de méthane

Formule développée de la molécule de méthane

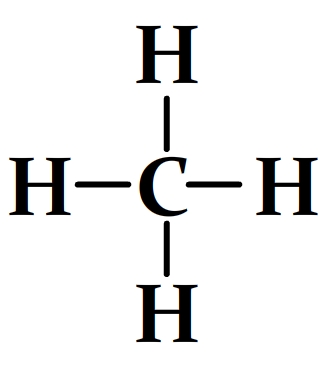
Cette molécule comprend:

• 4 liaisons carbone-hydrogène C-H dont l’énergie molaire de liaison est El(C-H) = 413 kJ.mol^-1

Par conséquent:

• El(méthane) = 4 x El(C-H)
• El(méthane) = 4 x 413
• El(méthane) = 1652 kJ.mol^-1

Calcul de l’énergie molaire de liaison de la molécule de propane

Formule développée de la molécule de propane:

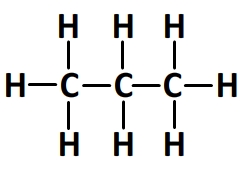
Cette molécule comprend:

• 8 liaisons carbone-hydrogène C-H dont l’énergie molaire de liaison est El(C-H) = 413 kJ.mol^-1
• 2 liaisons carbone-carbone C-C dont l’énergie molaire de liaison est El(C-C) = 346 kJ.mol^-1

Par conséquent:

• El(propane) = 8 x El(C-H) + 2 x El(C-C)
• El(propane) = 8 x 413 + 2 x 346
• El(propane) = 3996 kJ.mol^-1

Calcul de l’énergie molaire de liaison de la molécule de l’éthanol

Formule développée de la molécule de l’éthanol:

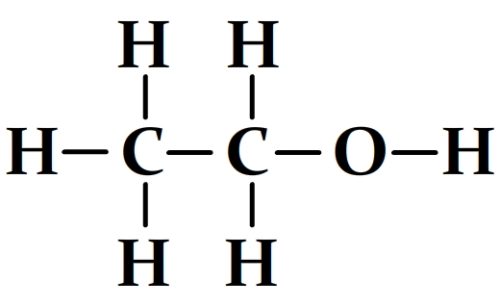
Cette molécule comprend:

• 5 liaisons carbone-hydrogène C-H dont l’énergie molaire de liaison est El(C-H) = 411 kJ.mol^-1
• 1 liaison carbone-carbone C-C dont l’énergie molaire de liaison est El(C-C) = 346 kJ.mol^-1
• 1 liaison Carbone oxygène C-O dont l’énergie molaire de liaison est El(C-O) = 358 kJ.mol^-1
• 1 liaison oxygène-hydrogène O-H dont l’énergie molaire de liaison est El(O-H) = 459 kJ.mol^-1

Par conséquent:

• El(éthanol) = 5 x El(C-H) + El(C-C) + El(C-O) + El(O-H)
• El(éthanol) = 5 x 411 + 346 + 358 + 459
• El(éthanol) = 3218 kJ.mol^-1

---

Energies de réaction

Définition de l’énergie molaire de réaction

L’énergie molaire de réaction se note E_R et s’exprime en joule par mole (J.mol^-1)

Pour une combustion l’énergie molaire de réaction correspond à l’énergie libérée par la combustion d’une mole de combustible.

Exemples

L’énergie molaire de la combustion de l’éthanol correspond à l’énergie libérée par la combustion d’une mole d’éthanol.

L’énergie molaire de combustion propane correspond à l’énergie que libère la combustion d’une mole de propane

etc…

C’est une énergie toujours négative car une combustion est exothermique et le système chimique libère de l’énergie.

Méthode n°1 pour calculer l’énergie molaire de réaction

Méthode n°1

Pour calculer l’énergie molaire d’une réaction de combustion on peut calculer la différence entre les énergies molaires de liaison des réactifs et les énergies molaires de liaison des produits.

Etape 1: écrire correctement l’équation de réaction

Dans un premier temps il est nécessaire d’écrire l’équation de réaction équilibrée de la combustion en veillant à attribuer au combustible un coefficient “1” (ce qui revient à ne pas noter de coefficient stoechiométrique) même si cela implique d’avoir des coefficients stoechiométriques à virgule (décimaux) pour d’autres réactifs ou produits.

Etape 2: Calculer les énergies molaires de liaisons des molécules

Calculer les énergies molaires de liaison de tous les réactifs et de tous les produits (voir méthode dans le paragraphe précédent “Energie molaire de liaison d’une molécule”.)

Etape 3: Calculer l’énergie molaire de liaison totale des réactifs

Il faut additionner l’énergie molaire de liaison de tous les réactifs en tenant compte des coefficients stoechiométriques. Le combustible a toujours un coefficient stoechiométrique de valeur “1” et donc son énergie molaire de liaison n’est comptée qu’une seule fois mais si un réactif a un coefficient “2” alors son énergie molaire est comptée deux fois dans le total, si son coefficient stoechiométrique est “3” alors il est compté trois fois etc

La somme des énergies molaires de liaison des molécules de réactif est notée ΣE_l(réactifs)

Etape 4: Calculer l’énergie molaire de liaison totale des produits

Il faut additionner l’énergie molaire de liaison de tous les produits en tenant compte des coefficients stoechiométriques.

La somme des énergies molaires de liaison des molécules de produits est notée ΣE_l(produits)

Etape 5: Calculer la différence entre l’énergie molaire de liaison des réactifs et des produits

L’énergie molaire de la réaction est obtenue en calculant la différence entre les deux énergies précédentes:

E_R = ΣE_l(réactifs) – Σe_l(produits)

Méthode n°2 pour calculer l’énergie molaire de réaction

Si les énergies molaires de liaison des molécules ne sont pas données mais qu’elles doivent être calculées à partir des énergies molaires de liaisons alors il peut être nettement plus rapide et simple de calculer l’énergie molaire de réaction en faisant directement la différence des énergies molaires des liaisons constituant les réactifs et les produits.

Etape 1: écrire correctement l’équation de réaction

Les consignes sont les mêmes que pour la méthode n°1, à savoir qu’il faut équilibrer l’équation de réaction en assignant un coefficient stoechiométrique “1” au combustible quitte à avoirs des coefficients avec virgules pour d’autres molécules de l’équation.

Etape 2: Calculer l’énergie molaire totale de toutes les liaisons présentes dans les réactifs

Il faut additionner l’énergie molaire de toutes les liaison des réactifs en tenant compte des coefficients stoechiométriques.

Si par exemple une liaison A-B est présente 4 fois dans un réactif de coefficient stoechiométrique “2” alors l’énergie El(A-B) est compté 4×2 = 8 fois dans le total (8 x El(A-B) ).

Si par exemple une liaison C-D est présente 5 fois dans un réactif de coefficient stoechiométrique “1” et 4 fois dans un autre réactif de coefficient “3” alors l’énergie El(C-D) est compté 5×1 + 4×3 = 17 fois dans le total (17 x El(C-D) )

Etape 3: Calculer l’énergie molaire totale de toutes les liaisons présentes dans les produits

Il faut additionner l’énergie molaire de toutes les liaison des produits en tenant compte des coefficients stoechiométriques.

Etape 4: Calculer la différence entre l’énergie molaire des liaison dans les réactifs et dans les produits

L’énergie molaire de la réaction est obtenue en calculant la différence entre les deux énergies précédentes. Cependant le calcul pourra se faire en simplifiant l’expression en tenant compte des énergies de liaisons présentes à la fois dans les produits et les réactifs.

Exemple – Calcul de l’énergie molaire de réaction pour la combustion du propane

Le propane est un alcane, sa combustion avec le dioxygène ne produit que du dioxyde de carbone et de l’eau.

Son équation (non équilibrée) est donc:

CH₃-CH₂-CH₃ + O₂ → H₂O + CO₂

L’équation de réaction équilibrée est:

CH₃-CH₂-CH₃ + 5 O₂ → 4 H₂O + 3CO₂

La molécule de propane a pour Formule développée:

Elle comporte

• 8 liaisons carbone-hydrogène C-H dont l’énergie molaire de liaison est El(C-H) = 413 kJ.mol^-1
• 2 liaisons carbone-carbone C-C dont l’énergie molaire de liaison est El(C-C) = 346 kJ.mol^-1

Par conséquent:

• El(propane) = 8 x El(C-H) + 2 x El(C-C)
• El(propane) = 8 x 413 + 2 x 346
• El(propane) = 3996 kJ.mol^-1

La molécule de dioxygène a pour Formule développée:

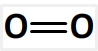
Elle ne comporte qu’une double liaison oxygène-oxygène O=O d’énergie molaire de liaison El(O=O) = 494 kJ.mol^-1

Par conséquent El(dioxygène) = El(O=O) = 494 kJ.mol^-1

La molécule de d’eau a pour Formule développée:

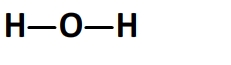
Elle comporte:

• 2 liaisons oxygène-hydrogène O-H dont l’énergie molaire de liaison est El(O-H) = 459 kJ.mol^-1

Par conséquent:

• El(eau) = 2 x El(O-H)
• El(eau) = 2 x 459
• El(eau) = 918 kJ.mol^-1

La molécule de dioxyde de carbone a pour Formule développée:

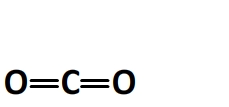
Elle comporte:

• 2 doubles liaisons carbone-oxygène C=O dont l’énergie molaire de liaison est El(C=O) = 795 kJ.mol^-1 (valeur spécifique au dioxyde de carbone)

Par conséquent:

• El(dioxyde de carbone) = 2 x El(C=0)
• El(dioxyde de carbone) = 2 x 795
• El(dioxyde de carbone) = 1590 kJ.mol^-1

Calcul de l’énergie molaire de la réaction de combustion du propane:

• E_R = ΣE_l(réactifs) – Σe_l(produits)
• E_R = El(propane) + 5El(dioxygène) – [ 4El(eau) + 3El(dioxyde de carbone) ]
• E_R = 3996 + 5 x 494 – [4 x 918 + 3 x 1590]
• E_R = -1976 kJ.mol^-1

Exemple – Calcul de l’énergie molaire de réaction pour la combustion de l’éthanol

L’éthanol est un alcool, sa combustion complète dans le dioxygène produit du dioxyde de carbone et de l’eau.

L’équation de réaction (non équilibrée) est:

CH₃-CH₂-OH + O₂ → H₂O + CO₂

L’équation de réaction équilibrée est:

CH₃-CH₂-OH + 3O₂ → 3H₂O + 2 CO₂

La molécule d’éthanol a pour Formule développée:

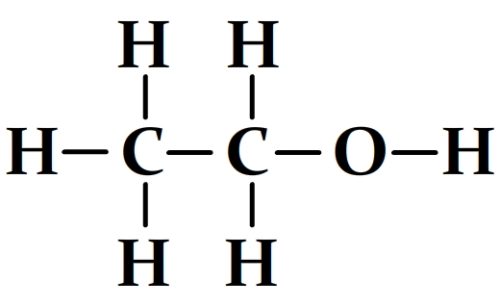
Elle comporte

• 5 liaisons carbone-hydrogène C-H dont l’énergie molaire de liaison est El(C-H) = 413 kJ.mol^-1
• 1 liaison carbone-carbone C-C dont l’énergie molaire de liaison est El(C-C) = 346 kJ.mol^-1
• 1 liaison C-O dont l’énergie molaire de liaison est El(C-C) = 358 kJ.mol^-1
• 1 liaison oxygène-hydrogène O-H dont l’énergie molaire de liaison est El(O-H) = 459 kJ.mol^-1

Par conséquent:

• El(éthanol) = 5 x El(C-H) + 1 x El(C-C) + 1 x El(C-O) + 1 x El(O-H)
• El(éthanol) = 5 x 413 + 1 x 346 + 1 x 358 + 1 x 459
• El(éthanol) = 3228 kJ.mol^-1

La molécule de dioxygène a pour énergie molaire de liaison El(dioxygène) = El(O=O) = 494 kJ.mol^-1 (voir exemple précédent pour le calcul)

La molécule de d’eau a pour énergie molaire de liaison El(eau) = 918 kJ.mol^-1 (voir exemple précédent pour le calcul)

La molécule de dioxyde de carbone a pour énergie molaire de liaison El(eau) = 1590 kJ.mol^-1 (voir exemple précédent pour le calcul)

Calcul de l’énergie molaire de la réaction de combustion de l’éthanol:

• E_R = ΣE_l(réactifs) – Σe_l(produits)
• E_R = El(éthanol) + 3El(dioxygène) – [ 3El(eau) + 2El(dioxyde de carbone) ]
• E_R = 3228 + 3 x 494 – [3 x 918 + 2 x 1590]
• E_R = -1224 kJ.mol^-1

Energie de réaction

Définition

L’énergie de réaction correspond à l’énergie libérée lors d’une réaction donnée

Elle se note “E” et s’exprime en Joule (J)

L’énergie de réaction est proportionnelle à:

• quantité de combustible consommé
• l’énergie molaire de réaction du combustible

Par conséquent elle peut être s’exprimer à partir de la relation suivante:

E = n x E_R

où:

• E est l’énergie de réaction (en joule)
• n est la quantité de matière (en mole)
• E_R est l’énergie molaire de réaction du combustible (en joule par mole)

Exemples de calcul d’énergie de réaction

• On Fait bruler 2,0 mol d’éthanol

son énergie de réaction est de -1224 kJ.mol^-1

L’énergie de réaction est exprimée par la relation E = n x E_R

soit E = 2,0 x (-1224)

E = -2448 kJ.mol^-1

Donc l’énergie de réaction est de E = -2448 kJ

• On Fait bruler 3,2 mol d’éthanol

E = n x E_R

E = 3,2 x (-1224) donc l’énergie de réaction est de E = 2448 kJ.mol^-1

E = -3916,8 kJ.mol^-1

Donc l’énergie de réaction est de E = -3216,8 kJ

• On Fait bruler 0,5 mol de propane

son énergie de réaction est de -1976 kJ.mol^-1

L’énergie de réaction est exprimée par la relation E = n x E_R

soit E = 0,5 x (-1976)

E = -988 kJ.mol^-1

Donc l’énergie de réaction est de E = -988 kJ

Pouvoir calorifique massique

Définition

Le pouvoir calorifique correspond à l’énergie libérée lors d’une combustion pour une unité de masse de combustible consommée (en général pour un kilogramme de combustible brûlé)

C’est une grandeur propre à chaque combustible et ne dépend que la nature de ce dernier. En d’autres termes chaque combustible possède son propre pouvoir calorifique massique.

Notation: PC (P pour pour Pouvoir et C pour Combustible)

Unité:

• le plus souvent en kilojoule par kilogramme (symbole kJ.kg^-1)
• parfois en mégajoule par kilogramme (symbole MJ.kg^-1)

Il peut être utilisé pour calculer l’énergie de réaction grâce à la relation suivante:

E = PC x m

où:

• E est l’énergie de réaction en kilojoule (kJ)
• PC est le pouvoir calorifique massique en kilojoule par kilogramme (kJ.kg^-1)
• m est la masse de combustible consommée en kilogramme (kg)

Calculer le pouvoir calorifique massique

La relation entre l’énergie de réaction et le pouvoir calorifique est la suivante:

E = PC x m

Par conséquent il est possible d’isoler et d’exprimer le pouvoir calorifique massique:

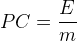
Si l’on est en mesure de déterminer l’énergie “E” dégagée pendant une combustion ainsi que la masse de combustible “m” consommée pendant cette combustion alors le pouvoir calorifique massique peut être calculé, il correspond au rapport de ces deux grandeurs:

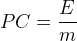
où:

• E est l’énergie de réaction en kilojoule (kJ)
• PC est le pouvoir calorifique massique en kilojoule par kilogramme (kJ.kg^-1)
• m est la masse de combustible consommée en kilogramme (kg)

Cette relation permet une détermination expérimentale de PC.

Le pouvoir calorifique massique peut aussi être calculé grâce à l’énergie molaire de réaction E_R.

Si l’on reprend l’expression précédente:

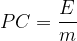
La masse “m” peut s’exprimer comme le produit de la masse molaire “M” par la quantité de matière “n”: m = M x n

La relation devient alors:

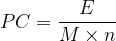
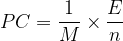
On remarque ici le rapport de l’énergie de réaction “E” par la quantité de matière “n” qui correspond à l’énergie molaire de réaction E_R.

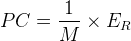
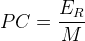
L’expression du pouvoir calorifique massique est donc:

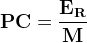
où:

• E_R est l’énergie molaire de réaction en kilojoule par mole (kJ.mol^-1)
• M est la masse molaire du combustible en kilogramme par mol (kg.mol^-1)
• PC est le pouvoir calorifique massique en kilojoule par kilogramme (kJ.kg^-1)

Par besoin de cohérence l’unité à utiliser pour la masse molaire “M” n’est l’unité usuelle.

Exemple

Calcul du pouvoir calorifique massique de l’éthanol

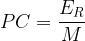
L’énergie molaire de réaction de l’éthanol est de

E_R = -1224 kJ.mol^-1

La masse molaire de l’éthanol est M = 2 x M(C) + 6xM(H) + M(O)

soit M(C₂H₆O) = 2 x 12 + 6 x 1 + 16

M(C₂H₆O) = 46 g.mol^-1

M(C₂H₆O) = 46.10^-3 kg.mol^-1

donc:

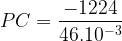
PC = 26,6 kJ.kg^-1

A réviser

Cours de seconde:

• Les espèces chimiques
• Vers des entités plus stables chimiquement
• Les doublets liants
• Notion d’énergie de liaison
• Transformation chimique
• Les transformations chimiques
• Les réactifs d’une transformation chimique
• Les produits d’une transformation chimique
• Ecrire et équilibrer une équation de réaction
• Stoechiométrie
• Transformations chimiques exothermiques et endothermiques

Les autres cours de première spécialité

• Quantité de matière, masse molaire et concentration
• Réaction d’oxydoréduction et avancement
• Titrage colorimétrique redox
• Schéma de Lewis, géométrie, électronégativité et polarisation
• Cohésion des solides, dissolution, solubilité, hydrophilie et lipophilie
• Structure et nomenclature des espèces organiques
• Synthèses d’espèces organiques

Pour approfondir et découvrir

• Pouvoir calorifique inférieur (PCI) et supérieur (PCS) de combustibles usuels – Université Environnement Développement Durable
• Formation et réserves de combustibles fossiles