Cours de physique-chimie | première spécialité
Ce cours correspond à la partie “1. Ondes mécaniques” du programme de première spécialité.
Il est situé dans la partie du programme “Ondes et signaux”
- Ondes mécaniques progressives
- Retard
- Célérité d’une onde
- Ondes mécaniques progressives périodiques
- Période et fréquence
- Longueur d’onde
- Relation entre longueur d’onde période et fréquence
- Ondes sinusoïdales
REVISER – AUTRES COURS DE PREMIERE SPECIALITE – APPROFONDIR ET DECOUVRIR
Ondes mécaniques progressives
Définition
Une onde mécanique progressive correspond à une perturbation qui se propage dans milieu matériel élastique
La perturbation correspond à une déformation du milieu matériel qui peut être :
- une variation locale de volume (compression/dilation)
- une élongation (pour un milieu linéaire comme une corde)
- une déformation de la surface (dépression, surélèvement)
Exemples d’Ondes mécaniques progressives :
- une vague (propagation d’une déformation de la surface de l’eau)
- le son (propagation d’une série de compressions-dépression de l’air)
Contrairement à d’autres types d’Ondes (les ondes électromagnétiques par exemple) les Ondes mécaniques ne peuvent pas se propager dans le vide, elles ont besoin de matière. Cette propriété est liée à leur nature : puisqu’elles correspondent à la propagation d’une déformation, il ne peut pas y avoir de déformation sans matière.
L’observation d’une onde progressive peut donner l’illusion d’un déplacement de matière mais chaque perturbation se forme en point différent de la précédente et se fait à partir d’une matière différente. La perturbation qui se propage dans milieu matériel ne provoque qu’un déplacement temporaire de la matière qui retrouve son emplacement initial lorsque la perturbation disparaît.
Par conséquent, une onde progressive ne s’accompagne pas d’un transport de matière.
Pour simplifier on pourrait dire que la matière ne suit pas le trajet de la perturbation. Par contre lorsque la perturbation qui se propage au sein de la matière modifie (temporairement aussi) l’énergie mécanique de celle-ci et donc :
Une onde progressive s’accompagne d’une transmission d’énergie.
Voir cours Les ondes
Le retard
- Notation : τ (lettre grecque tau minuscule)
- Unité : seconde (s)
Définition
Si deux points M1 et M2 sont atteints successivement par une perturbation respectivement aux temps t1 et t2 alors le retard entre ces points correspond à la durée τ = t2 – t1
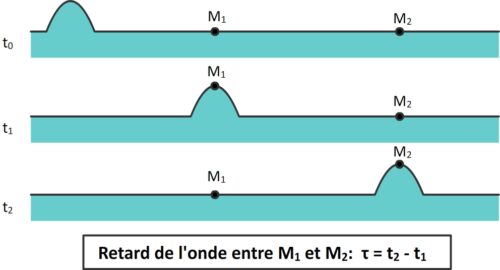
Un retard est donc toujours exprimé entre deux points par lesquels « passe » une onde. Il correspond à la durée que l’onde met pour se propager du premier point au deuxième.
Célérité d’une onde
Notation : v (comme une vitesse)
Unité : mètre par seconde symbole m.s-1 (comme une vitesse)
Définition
La célérité d’une onde correspond à la vitesse à laquelle se propage une onde mécanique dans un milieu matériel donné.
Calculer la célérité d’une onde
La célérité correspond au rapport de la distance sur laquelle s’est propagée une perturbation par la durée de cette propagation. On peut en particulier l’exprimer comme le rapport de la distance entre deux points M1 et M2 par le retard de l’onde entre ces deux points :
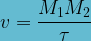
La célérité d’une onde dépend :
- de la nature de l’onde
- de la composition du milieu (en particulier de l’état physique)
- des paramètres physiques du milieu (en particulier, la température, la pression et la densité)
Calculer la distance sur laquelle se propage une perturbation
Si une perturbation se propage pendant une durée « Δt » avec une célérité « v » alors la distance « d » parcourue par la perturbation est :
d = v x Δt
Calculer la durée de propagation
Si une perturbation se propage sur une distance « d » avec une célérité « v » alors la durée de la propagation est donnée par la formule :
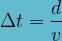
Ondes mécaniques progressives périodiques
Définition
On dit qu’une onde mécanique progressive est périodique si chaque point du milieu de propagation subit des perturbations identiques à des intervalles de temps constants.
Une onde mécanique ne peut être périodique que si le phénomène qui produit cette onde est lui même périodique
Voir cours Les phénomènes périodiques
Période et fréquence
La période d’une onde mécanique périodique :
- se note « T » ( comme la période de n’importe quel phénomène périodique)
- a pour unité la seconde (s)
Définition de la période
La période correspond à la durée qui s’écoule entre le passage de deux perturbations successives par le même point d’un milieu de propagation.
La fréquence d’une onde mécanique périodique :
- se note « f »
- a pour unité le hertz (Hz)
Définition de la fréquence
La fréquence correspond au nombre de périodes que comporte une durée d’une seconde.
La fréquence correspond aussi au nombre de perturbations qui atteignent un même point du milieu de propagation pendant une durée d’une seconde.
Calculer la fréquence à partir de la période :
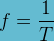
où :
Calculer la période à partir de la fréquence :
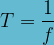
où :
Voir cours La période – La fréquence
Longueur d’onde
Notation :λ (lettre grecque lambda)
Unité : mètre (m)
Définition
Lorsqu’une onde mécanique progressive est périodique alors la distance qui sépare deux perturbations successives correspond à la longueur d’onde.
Plus précisément la longueur d’onde est la distance qui sépare deux points successifs en phases, c’est à dire dans le même état vibratoire (la valeur de la déformation ainsi que le sens dans lequel elle évolue sont identiques).
La longueur d’onde correspond aussi à la distance sur laquelle se propage la perturbation pendant une durée d’une période.
Relation entre longueur d’onde période et fréquence
La distance de propagation d’une onde est donnée par la relation :
d = v x Δt
Si la durée Δt correspond à une période (T) alors distance de propagation correspond à la longueur d’onde λ par conséquent :
λ = v x T
Etant donné que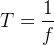 
alors la longueur d’onde peut aussi être exprimée en fonction de la fréquence :
λ = v x T
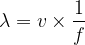
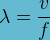
Ondes sinusoïdales
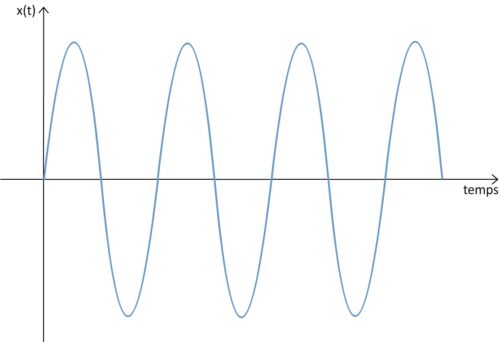
Une onde mécanique progressive périodique est sinusoïdale si la grandeur physique qui caractérise la perturbation varie en suivant une fonction sinusoïdale.
Le graphique qui représente l’évolution de cette grandeur au cours du temps prend toujours l’aspect d’une succession de vagues d’amplitudes et de durées constante
A réviser
Cours de seconde:
- Emission et perception d’un son
- Les ondes
- Les ondes sonores
- Les phénomènes périodiques
- La période
- La fréquence
Les autres cours de première spécialité
- Quantité de matière, masse molaire et concentration
- Réaction d’oxydoréduction et avancement
- Titrage colorimétrique redox
- Schéma de Lewis, géométrie, électronégativité et polarisation
- Cohésion des solides, dissolution, solubilité, hydrophilie et lipophilie
- Structure et nomenclature des espèces organiques
- Synthèses d’espèces organiques
- L’énergie de la matière organique
- Interactions, champs électrostatiques et gravitationnels
- Statique des fluides
- Variations de vecteur vitesse
- Courant électrique et bilans énergétiques
- Energies cinétiques, potentielles et mécaniques
Pour approfondir et découvrir
- L’énergie cinétique – C’est pas sorcier (Youtube)