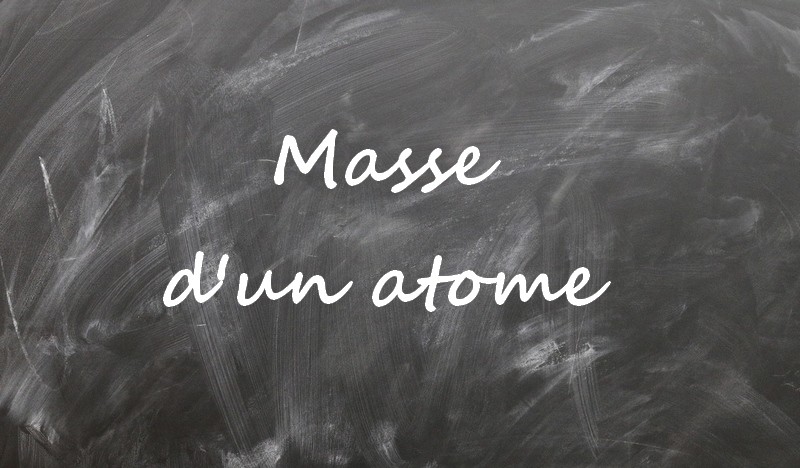Masse d’un atome

Cours de chimie niveau seconde – Constitution et transformations de la matière – Partie 1: de l’échelle macroscopique à l’échelle microscopique – B) Modélisation de la matière à l’échelle microscopique – Le noyau de l’atome, siège de sa masse et de son identité

• Masse des nucléons
• Masse d’un noyau atomique
• Masse des électrons
• Masse du cortège électronique
• Comparaison de la masse du noyau et du cortège électronique
• Calculer la masse d’un atome
• Calculer la masse d’un ion monoatomique
• Pour aller plus loin: le défaut de masse

Masse des nucléons

Les nucléons sont les particules qui constituent les noyaux atomiques, il en existe deux sortes: les protons et les neutrons.

La masse précise d’un proton est de m_proton = 1,6726231 x 10^-27 kg (source UICPA)
La masse précise d’un neutron est de m_neutron = 1.674 9286 x 10^-27 kg (source UICPA)

Le proton et le neutron ont des masses très proches mais pas exactement égales néanmoins, si l’on se, contente d’exprimer ces deux masses avec trois chiffres significatifs alors on peut faire l’approximation qu’elles ont une valeur commune de 1,67 x 10^-27 kg.

On peut retenir que la masse d’un nucléon (proton ou neutron) est d’environ:

m_n = 1,67x 10^-27 kg

Masse d’un noyau atomique

La masse d’un noyau d’atome peut être calculée en additionnant la masse de tout ses composants: les neutrons et les protons.
Le nombre de protons d’un noyau correspond au numéro atomique Z tandis que le nombre de neutrons correspond à la différence du nombre de masse et du numéro atomique (A-Z). Par conséquent la masse précise d’un noyau atomique peut être obtenue grâce au calcul:

m_atome = Z x m_proton + (A-Z) x m_neutron

Ce calcul peut être simplifié si l’on fait l’approximation que les neutrons et les protons ont la même masse (voir paragraphe précédent). Dans ce cas la masse totale du noyau correspond au produit du nombre de masse par la masse d’un nucléon:

m_atome = A x m_n

avec:

• m_atome la masse de l’atome (en kg)
• A nombre de masse
• m_n= 1,67x 10^-27 kg, la masse d’un nucléon

Exemples

• La masse du noyau de l’isotope 12 du carbone (A = 12) est:
  m_nC = A x m_n
  m_nC = 12 x 1,67x 10^-27
  m_nC = 2,00.10^-26 kg
• La masse du noyau de l’isotope 235 de l’uranium (A=235) est:
  m_nU = A x m_n
  m_nU = 235 x 1,67x 10^-27
  m_nU = 3,92.10^-25 kg

Masse des électrons

La masse précise d’un électron est:

 m_e = 9.109 3897 x 10^-31 kg

(source UICPA)

Masse du cortège électronique

Un atome étant électriquement neutre la charge négative des électrons et la charge positive du noyau se compensent. Il y a donc, dans un atome, autant d’électrons que de protons et le numéro atomique Z correspond aussi au nombre d’électron.

La masse “m” du cortège électronique d’un atome est donc le produit du numéro atomique de cet atome par la masse de l’électron:

m_cort = Z x m_e

où:

• m_cort est la masse du cortège électronique (en kg)
• Z est le numéro atomique de l’atome
• m_e est la masse d’un électron (m_e = 9.109 3897 x 10^-31 kg)

Exemples

• L’atome de carbone (Z=12) a un cortège électronique de masse:
  m_cort(C) = Z x m_e
  m_cort(C) = 12 x 9.109 3897 x 10^-31
  m_cort(C) = 1,093 1268 x 10^–29 kg
• L’atome d’uranium (Z=92) a un cortège électronique de masse:
  m_cort(U) = Z x m_e
  m_cort(U) = 92 x 9.109 3897 x 10^-31
  m_cort(U) = 8,380 6385 x 10^–29 kg

Comparaison de la masse du noyau et du cortège électronique

La masse d’un nucléon (composant du noyau) est de m_n = 1,67x 10^-27 kg
La masse d’un électron (composant du cortège électronique) est de m_e = 9.10 x 10^-31 kg
Le rapport de masse d’un nucléon par celle d’un électron est donc:

 

 

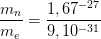
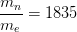
La masse d’un nucléon est près de 2000 fois plus grande que celle d’un électron.

 

Par ailleurs le nombre d’électrons n’excède jamais celui de nucléons puisqu’il correspond au nombre de protons alors que les nucléons incluent les protons mais aussi les neutrons.

Par conséquent la masse du cortège électronique est négligeable devant celle du noyau:

la masse d’un atome se concentre dans son noyau.

 

Calculer la masse d’un atome

Le calcul approximatif de la masse d’un atome peut être fait en ajoutant la masse de ses différents composants.

Si l’on se contente d’une valeur de masse comportant trois chiffres significatifs alors on peut faire deux approximations:

• Les nucléons (protons et nucléons) ont la même masse soit m_n= 1,67x 10^-27 kg
• La masse des électrons est négligeable devant celle du noyau

On peut alors considérer que la masse de l’atome correspond à celle de son noyau et l’on peut alors la calculer on multipliant le nombre de nucléons (A) par la masse d’un nucléon (m_n):

m_atome = A x m_n

où:

• m_atome est la masse de l’atome (en kg)
• m_n est la masse d’un nucléon (avec 1,67x 10^-27 kg)
• A est le nombre de masse (nombre de nucléons)

Exemples

• Masse d’un atome d’aluminium (A=27):
  m(Al)= A x m_n
  m(Al)= 27 x 1,67x 10^-27
  m(Al)= 4,51.10^-26 kg
• Masse d’un atome de fluor (A=19):
  m(F)= A x m_n
  m(F)= 19 x 1,67x 10^-27
  m(F)= 3,17.10^-26 kg

Calculer la masse d’un ion monoatomique

Un ion monoatomique ne diffère d’un atome que par un défaut ou un excès d’électrons, or ces derniers peuvent être négligés dans le calcul de la masse d’un atome par conséquent ils peuvent aussi l’être dans le calcul de la masse d’un ion:

La masse d’ion correspond à celle de son noyau

Un ion monoatomique possède la même masse que l’atome dont il est issu.

Un ion monoatomique de nombre de masse A a une masse:

m_ion = A x m_n

 

Pour aller plus loin: le défaut de masse

Si l’on compare avec précision la masse d’un noyau atomique et celle de ses nucléons pris séparément alors on obtient une différence:

La masse d’un noyau où les nucléons son liés ensembles est toujours légèrement inférieure à la masse de ses nucléons lorsqu’ils sont séparés et indépendants.

Cette différence est qualifiée de “défaut de masse”

Où est passée cette masse ? Une partie de la masse des nucléons a été convertie en une énergie de liaison qui permet de maintenir ces nucléons ensembles.

C’est la célèbre formule“E=m.c²” qui rend compte de la possible conversion de la masse en énergie (ou de l’inverse).

Dans la plupart des noyaux atomiques le défaut de masse est proche de 1%, c’est à dire que la masse réelle d’un noyau a une masse inférieure d’environ 1% à la masse totale de ses nucléons isolés.