Interactions, champs électrostatiques et gravitationnels

04/08/202228/02/2021 par Prof

Cours de physique-chimie | première spécialité

Ce cours correspond à la partie “Interactions fondamentales et introduction à la notion de champ” du programme de première spécialité.

Il est situé dans la partie du programme “Mouvement et interactions”

Notion de charge électrique
Charge électrique élémentaire
Particules électriquement chargées
Electrisation de la matière
Interaction électrostatique
Loi de Coulomb
Exemples d’utilisation de la loi de Coulomb
Comparaison de loi de Coulomb et de loi d’interaction gravitationnelle
Notion de champ
Champ de gravitation
Champ de pesanteur
Champ électrostatique

REVISER – AUTRES COURS DE PREMIERE SPECIALITE – APPROFONDIR ET DECOUVRIR

Notion de charge électrique

Qu’est ce que la charge électrique ?

C’est une caractéristique propre à la matière au même titre que la masse.

Toute matière (particule ou matière macroscopique) possède une charge électrique qui peut être:

Positive
Négative
De valeur variable
éventuellement nulle

Une charge électrique se note “Q” ou “q”

Son unité est le Coulomb de symbole “C” choisie en hommage à Charles Coulomb

Si par exemple un corps possède une charge négative de 3,2.10^-19 Coulomb alors on peut la noter de la manière suivante:

q = – 3,2.10^-19 C

Voir aussi cours sur la charge électrique

La charge électrique élémentaire

La charge électrique élémentaire est une charge électrique particulière:

il s’agit de la plus petite valeur qu’une charge électrique peut prendre.

La charge électrique élémentaire se note “e” ( “e” comme élémentaire ) et a pour valeur e = 1,6.10^-19 C

Par conséquent tout corps électriquement chargé (c’est à dire de charge non nulle) possède une charge dont la valeur absolue est supérieure à 1,6.10^-19 C

Par ailleurs toute charge électrique est un multiple de la charge électrique élémentaire.

Si corps possède une charge “Q” positive alors on peut l’exprimer comme le produit d’un nombre entier de charges élémentaires:

Q = n x e

où:

“n” est un nombre entier
“e” est la charge élémentaire
“Q” est la charge que possède le corps

Pour un corps dont la charge “Q” est négative alors cette relation devient:

Q = – n x e

Pour simplifier il n’est pas rare que la charge d’un corps soit exprimée en nombre de charges élémentaires.

Par exemple la charge indiquée dans la formule d’un ion est en réalité un nombre de charges élémentaires. Ainsi les deux charges positives portées par un ion cuivre Cu²⁺ sont deux charges élémentaires positives et la charge totale d’un ion cuivre est 2 x e = 3,2.10^-19 C

Particules électriquement chargées

Particule	Charge (en nombre de charges élémentaires)	Charge électrique (en Coulomb)
proton	+e	1,6.10^-19 C
neutron	0	0 C
électron	-e	-1,6.10^-19 C
photon	0	0 C
Noyau atomique	Z x e	Z x 1,6.10^-19 C
Particule α	2e	3,2.10^-19 C

Electrisation de la matière

Qu’est-ce qu’une électrisation ?

C’est un phénomène au cours duquel une matière initialement neutre acquière une charge électrique.

Attention le terme “électrisation” peut avoir un sens différent, il peut aussi désigner le passage d’un courant électrique à travers le corps humain.

Quelles sont les différentes sortes d’électrisation ?

Les trois principales sortes d’électrisation sont l’électrisation par frottement, par contact et par influence.

Qu’est-ce que l’électrisation par frottement ?

Lors du frottement de deux matériaux isolants l’un contre l’autre il peut y avoir transfert d’électrons (et donc de charge électrique) de l’un vers l’autre.

Par exemple si l’on frotte une baguette en verre avec de la laine alors il y a un transfert d’électrons des fibres de laine vers le verre: la laine se charge positivement et le verre se charge négativement.

Qu’est-ce que l’électrisation par contact ?

Elle se produit lorsqu’un corps électriquement chargé est en contact avec un corps non chargé et conducteur électrique (comme un métal). Un simple contact suffit alors pour qu’il y ait un transfert d’électrons.

Qu’est-ce que l’électrisation par influence?

Elle se produit lorsqu’un corps électriquement chargé est proche d’un corps électriquement neutre. Ce dernier reste globalement neutre mais il apparaît localement une charge Q sur une face du corps et une charge de signe opposé -Q sur l’autre face. Ces charges apparaissent sous l’influence du corps chargé qui modifie l’orientation des molécules polaire (dans un isolant) ou provoque une migration d’électrons libre (dans un conducteur)

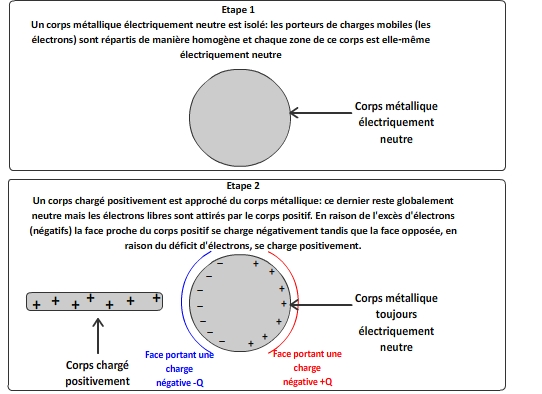
électrisation par influence

Le chargement part influence est relativement bien décrit pans cette vidéo; https://www.youtube.com/watch?v=My0Sa0q5MeI (Editions Larousse)

L’interaction électrostatique

Lorsque deux corps au repos (immobiles dans le référentiel d’étude) possèdent chacun une charge électrique non nulle alors il existe entre eux une interaction dite électrostatique:

Chaque corps exerce sur l’autre une force électrostatique aussi appelée force de Coulomb ou simplement force électrique.

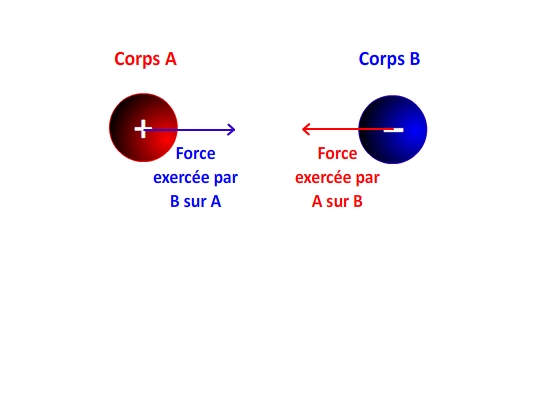
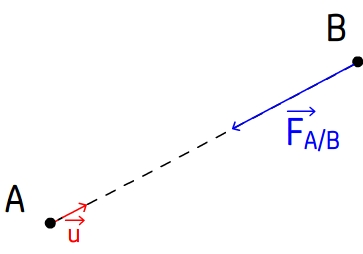
Force exercée par le corps A sur le corps B

Lorsque l’interaction s’exerce entre un corps “A” de charge q_Asitué en point “A” de l’espace et un corps “B” de charge q_B situé en un point “B” de l’espace alors les caractéristiques de la force exercée par le corps A sur le corps B sont les suivantes:

son point d’application se trouve au point “B” de l’espace
sa direction correspond à la droite (AB)
son sens dépend du signe de la charge q_A et de la charge q_B
sa valeur est donnée par la loi de Coulomb (voir paragraphe de ce cours consacré à la loi de Coulomb)

Force exercée par le corps B sur le corps A

Lors d’une interaction les forces exercées par les systèmes qui interagissent possèdent la même direction, la même valeur et des sens opposés, par conséquent la force électrostatique F_B/A exercée le corps B sur le corps A a les caractéristiques suivantes:

son point d’application se trouve au point A
sa direction correspond aussi à la droite (AB)
son sens est l’opposé de celui de la force F_A/B (et dépend donc du signe des charges q_A et q_B)
sa valeur est la même que celle de F_A/B ( donc donnée par la loi de Coulomb)

Les deux corps ont des charges de même signe

Si les deux corps qui interagissent ont une charge de même signe (ils sont tous les deux chargés positivement ou alors tous les deux chargés négativement) alors l’interaction est répulsive.

C’est à dire que les forces qui s’exerces tendent à éloigner les deux corps l’un de l’autre:

La force 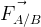$\text{[math]}$ est orientée de A vers B

La force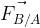 $\text{[math]}$ est orientée de B vers A

électrisation par influence — Interaction électrostatique entre des charges de signes identiques

Les deux corps ont des charges de signes opposés

Si les deux corps qui interagissent ont des charges de signes opposés (l’un est chargé positivement et l’autre négativement) alors l’interaction est attractive.

C’est à dire que les forces qui s’exerces tendent à rapprocher les deux corps l’un de l’autre:

La force 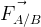$\text{[math]}$ est orientée de B vers A

La force 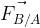$\text{[math]}$ est orientée de A vers B

Interaction électrique entre une charge positive et une charge négative — Interaction électrostatique entre une charge positive et une charge négative

Loi de Coulomb

La loi de Coulomb permet d’exprimer la force électrique exercée par corps électriquement chargé sur un autre corps électriquement chargé.

On considère la situation suivante:

un corps “A” modélisé par un point (ayant une taille assez petite pour être décrit par un point) est situé en un point A de l’espace et posséde une charge q_A.
Un corps “B”, lui aussi modélisé par un point, est situé en un point B de l’espace et possède une charge électrique q_B.
La distance AB qui sépare les deux corps est notée “r”.

D’après la lois de Coulomb l’expression de la force électrostatique F_A/B exercée par le corps A sur le corps B est la suivante:

$\text{[math]}$

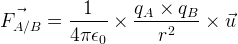
Dans cette formule:

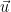$\text{[math]}$ est un vecteur unitaire (c’est à dire dont la longueur vaut une unité) ayant même direction que l’axe AB et orienté de A vers B
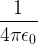$\text{[math]}$ est une constante (parfois simplement notée “k”) appelée constante de Coulomb avec 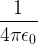$\text{[math]}$ = 8,99.10⁹ N.m².C^-2

Remarque: le terme ε₀(Epsilon zéro) correspond à la perméabilité électrique du vide

qA est la charge du corps A en Coulomb (C)
qB est la charge du corps B en Coulomb (C)
r est la distance entre le corps A et le corps B en mètre (m)
est la force exercée par le corps A sur le corps B. Sa valeur est en Newton, sa direction est celle du vecteur unitaire, son sens est le même que celui du vecteur unitaire si les deux charges même signe, son sens est l’inverse de celui du vecteur unitaire si les deux charges ont des signes différents.

Vecteur unitaire force de gravitation

Pour calculer l’intensité de la force électrostatique alors on peut utiliser la relation suivante qui dérive de la loi de Coulomb:

$\text{[math]}$

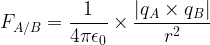
Dans cette formule | q_A x q_B | correspond à la valeur absolue du produit q_A x q_B

Exemples d’utilisation de la loi de Coulomb

Force exercée par le noyau d’un atome d’hydrogène sur l’électron de cet atome

Le corps A est ici le noyau de l’atome d’hydrogène.

Cet atome a comme numéro atomique Z=1 par conséquent le noyau ne comporte qu’un seul proton et ne possède qu’une seule charge élémentaire positive: q_A = e = 1,6.10^-19 C

Le corps B est l’électron qui possède une charge électrique élémentaire négative: q_B = -e = -1,6.10^-19 C

La distance entre le noyau d’hydrogène et son électron correspond au rayon de l’atome d’hydrogène qui vaut r=0,053 nm soit r = 5,3.10^-11 m

On commence par rappeler l’expression générale de la loi de Coulomb:

$\text{[math]}$

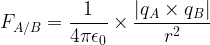
Chaque grandeur est remplacée par sa valeur numérique en respectant les unités (en particulier en s’assurant que la distance est bien exprimée en mètre):

$\text{[math]}$

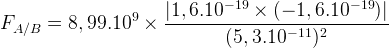
On applique la valeur absolue en supprimant le signe des charges multipliées:

$\text{[math]}$

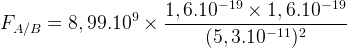
On effectue le caclul (à la calculatrice)

F_A/B= 8,2.10^–⁸N

Force électrostatique exercée par un ion cuivre Cu²⁺ sur un ion chlorure Cl^– distant de 12 mm

Le corps A est un ion cuivre caractérisé par un défaut de deux électrons, sa charge est:

q_A = 2 x e

q_A = 2 x 1,6.10^-19

q_A = 3,2.10^-19 C

Le corps B est un ion chlorure caractérisé par un excès d’un électron, sa charge est:

q_B = -e

q_B = -1,6.10^-19 C

La distance est r = 12 mm, soit r = 12.10^-3 m

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

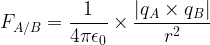
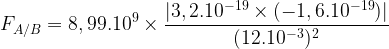
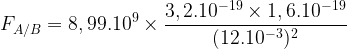
F_A/B= 3,2.10^-24N

Comparaison de loi de Coulomb et de loi d’interaction gravitationnelle

Rappels

Loi de coulomb (expression de la force électrostatique exercée par un corps A sur un corps B):

$\text{[math]}$

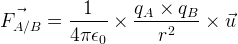
La valeur de la force électrostatique est:

$\text{[math]}$

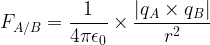
ou encore:

$\text{[math]}$

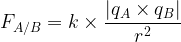
Loi de la gravitation universelle (expression de la force de gravitation exercée par un corps A sur un corps B):

$\text{[math]}$

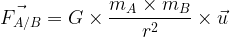
La valeur de la force de gravitation est:

$\text{[math]}$

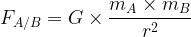
Les points communs:

La valeur de ces forces est proportionnelle à une grandeur propre aux corps qui interagissent (les charges pour la force électrostatique et les masses pour la force de gravitation)
La valeur de ces forces est inversement proportionnelle au carré de la distance qui sépare les corps (car on trouve r² au dénominateur). Par conséquent la valeur des deux forces est divisée par 2² (=4) lorsque la distance entre les corps est multipliée par 2, la valeur de ces deux forces est divisée par 3² (=9) lorsque la distance est multipliée par 3 etc.
Une constante de proportionnalité intervient dans chacune de ces lois ( La constante de Coulomb “k” pour la force électrostatique et la constante de gravitation “G” pour la force de gravitation).
Dans les deux cas la direction de la force correspond à celle de la droite (AB) qui joint les deux corps.

Différences:

Une masse est toujours une grandeur positive tandis qu’une charge électrique peut être positive ou négative. Il en résulte que la force de gravitation est toujours attractive alors que la force électrostatique peut être soit attractive (charges de signes différents) ou répulsive (charges de même signe)
A l’échelle de particules chargées (protons, électrons et même noyaux atomiques) la valeur de la force électrostatique est toujours nettement supérieure à celle de la force de gravitation.

Notion de champ

Définition

Un champ est une grandeur physique définie en tous point d’un espace donné.

Par exemple on peut utiliser la notion de champ pour des grandeurs telles que la température, la vitesse d’écoulement d’un fluide.

On distingue deux sortes de champs:

Les champs scalaires sont relatifs à une grandeur physique “scalaire” c’est dire exprimée par une simple valeur numérique (température, pression, masse volumique….)
Les champs vectoriels sont relatifs à une grandeur physique “vectorielle” c’est à dire qui peut être associée à un vecteur (vitesse, force…)

Si un champ est vectoriel alors il est possible de représenter des lignes de champs

Définition

Une ligne de champ est une ligne tangente au vecteur champ en chacun de ses points et orientée dans le même sens que ce dernier.

Propriétés:

Dans une région de l’espace les lignes de champs sont d’autant plus ressérées que le champ est intense.
Si dans une région de l’espace les lignes de champs sont toutes parallèles les unes aux autres alors le champs y est uniforme, il garde en tout point de cet espace la même valeur, la même direction et le même sens.

Voir cours sur les lignes de champs

Voir cours sur les champs scalaires et vectoriels

Champ de gravitation

Notation et unité

Le champ de gravitation est noté 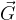$\text{[math]}$

Il est possible de préciser le point (M) de l’espace considérer en notant 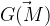$\text{[math]}$

Attention à ne pas le confondre avec la constante de gravitation (G).

Son unité est le newton par kilogramme de symbole N.kg^-1

Définition

Le champ de gravitation produit par un corps A en un point M de l’espace correspond au rapport de la force gravitation qu’exercerait le corps A sur un corps de B de masse m_B situé en ce point M de l’espace divisée par la masse m_B.

On peut l’exprimer par la relation suivante:

$\text{[math]}$

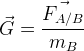
Valeur du champ de gravitation

Etant donné que la valeur de la force de gravitation qu’exerce un corps ponctuel A sur un corps B est donnée par la relation suivante:

$\text{[math]}$

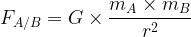
On peut en déduire la valeur du champ de gravitation d’un corps A:

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

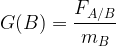
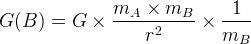
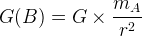
où:

G(B) est la valeur du champ de gravitation au point B en N.kg^-1
G est la constante de gravitation ( G = 6,67.10^-11 N.m².kg^-2)
mA est la masse du corps qui produit le champ de gravitation en kg
r est la distance entre le corps A (qui produit le champ) et le point B (où est exprimée la valeur du champ) en mètre

Sens et direction

Etant donné que la force de gravitation est toujours attractive le champ de gravitation a même sens et direction que 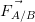$\text{[math]}$

Le champ de gravitation que produit un corps A en un point M de l’espace, a même direction que la droite (AM) et il est toujours orienté vers le corps qui produit le champ (de M vers A)

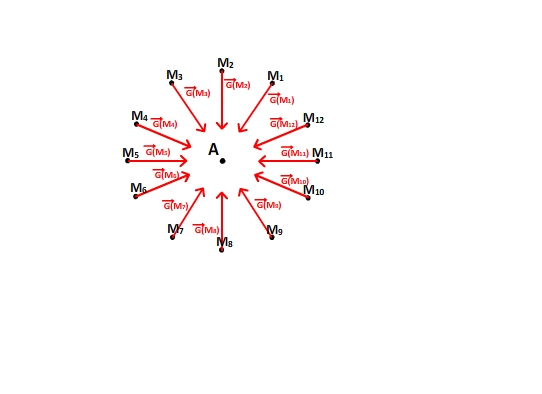
Champ de gravitation — champ de gravitation produit par un corps ponctuel

Les lignes de champs

Pour un corps ponctuel les lignes de champ de gravitation sont des droites qui passent par ce point et sont orienté vers lui.

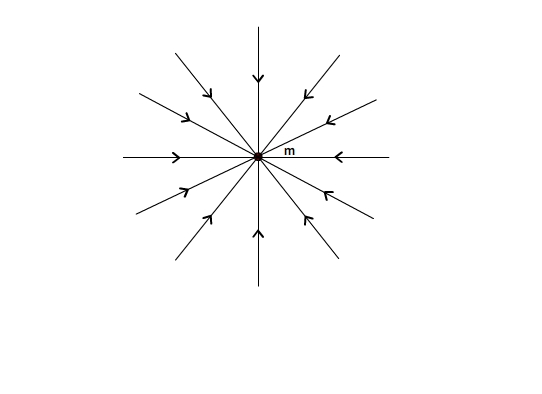
Lignes de champ d'un champ de gravitation

Voir cours sur le champ de gravitation

Champ de pesanteur

Notation et unité

Le champ de pesanteur est noté 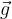$\text{[math]}$

Son unité est la même que celle du champ de gravitation c’est à dire le newton par kilogramme de symbole N.kg^-1

Définition

Le champ de pesanteur en un point M de l’espace correspond au rapport du Poids 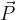$\text{[math]}$ qu’aurait en ce point un corps A de masse m_A divisé par cette masse m_A.

On peut l’exprimer par la relation suivante:

$\text{[math]}$

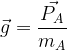
Le poids d’un corps résulte principalement de la force de gravitation exercée par la Terre, il en résulte que le champ de pesanteur correspond à un champ de gravitation local proche de la surface d’un astre.

Sens et direction valeur

Le champ de pesanteur est un champ uniforme: en tout point il possède toujours la la même direction, le même sens et la même valeur.

Le champ de pesanteur est vertical, orienté vers le bas et a pour valeur g = 9,81 N.kg^-1 (sur Terre)

Champs de pesanteur — Champ de pesanteur terrestre

Les lignes de champs

Les lignes d’un champ de pesanteur sont toujours verticales et orientées vers le bas

Voir cours sur le champ de gravitation

Champ électrostatique

Notation et unité

Le champ électrostatique (parfois aussi appelé champ simplement électrique) est noté E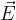 $\text{[math]}$ On peut aussi le noter 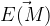$\text{[math]}$ où M est le point de l’espace où le champ est exprimé.

Son unité est le Newton par coulomb de symbole N.C^-1(Le volt par mètre V.m^-1 est une unité équivalente parfois également utilisée)

Définition

Le champ électrostatique produit par un corps A de charge q_A en un point M de l’espace correspond au rapport de la force électrostatique qu’exercerait ce corps A sur un corps de B de charge q_B situé en ce point M divisée par la charge q_B.

On peut l’exprimer par la relation suivante:

$\text{[math]}$

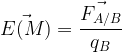
Valeur du champ électrostatique

Etant donné que la valeur de la force électrostatique qu’exerce un corps A sur un corps B est donnée par la relation suivante:

$\text{[math]}$

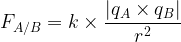
En utilisant la définition du champ électrostatique il est possible d’exprimer sa valeur:

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

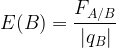
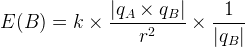
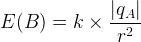
où:

E(B) est la valeur du champ électrostatique au point B en newton par coulomb (N.C^-1)
k est la constante de Coulomb ( k = 9,0.10⁹ N.m².kg^-2)
q_A est la charge électrique du corps qui produit le champ électrostatique en Coulomb (C)
r est la distance entre le corps A (qui produit le champ) et le point B (où est exprimée la valeur du champ) en mètre.

Sens et direction

Le champ électrostatique 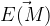$\text{[math]}$ produit par un corps A, de charge q_A en un point M de l’espace a même direction que la droite (AM).

Le champs électrostatique a même direction que la droite joignant le corps ponctuel chargé et le point M où le champ électrostatique est produit par ce corps.

L’expression vectorielle du champ électrostatique est la suivante:

$\text{[math]}$

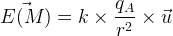
D’après cette expression, le sens du champ électrostatique dépend du signe de la charge électrique q_A possédée par le corps produisant le champ.

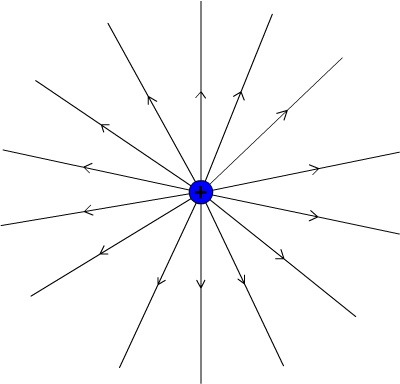
Lorsque le champ électrostatique est produit par un corps chargé positivement (qA>0) alors le 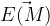$\text{[math]}$ pointe à l’opposé du corps chargé (possède même direction que le segment [AM]).

Par contre, lorsqu’un corps chargé négativement produit le champ alors il pointe en direction du corps chargé (le champ électrostatique 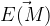$\text{[math]}$ a même direction que le segment [MA]).

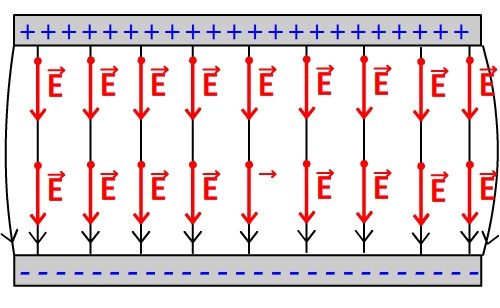
Champ électrique d'un condensateur — Champ électrique uniforme dans un condensateur plan

Les lignes de champs

Si le corps chargé est ponctuel alors les lignes de champs électrostatiques sont des droites passant par ce corps. Elles sont orientées vers lui si sa charge est négative et s’en éloignent si sa charge est positive.

Lignes du champ électrique d'une charge positive — Lignes du Champ électrique d’une charge positive

Voir:

A réviser

Cours de seconde:

Les autres cours de première spécialité

Pour approfondir et découvrir

Electrisation par influence – Vidéo Editions Larousse