Constitution et transformations de la matière – 1. Déterminer la composition d’un système par des méthodes physiques et chimiques – B) Analyser un système chimique par des méthodes physiques
- pH-métrie
- Conductivité et loi de Kohlrausch
- Spectroscopie UV – Loi de Beer-Lambert
- Spectroscopie infrarouge
- Dosage par étalonnage
- Déterminer la quantité de matière d’un gaz
pH-métrie
La mesure du pH d’une solution aqueuse permet d’accéder à la concentration en ions oxonium H3O+ de celle-ci. En effet, le pH est défini à partir de cette concentration par la relation suivante:
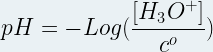
avec:
- [H3O+] concentration en ion oxonium (mol.L-1)
- c° concentration standard, c° = 1 mol.L-1
- pH sans unité
En exploitant la fonction réciproque du logarithme décimal (Log) Il est possible d’exprimer la concentration en ions oxonium à partir du pH:
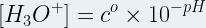
Ainsi, par exemple:
- dans une solution où pH = 1 on a une concentration:
[H3O+] = 10 -1/1
[H3O+] = 10-1 mol.L-1
[H3O+] = 0,1 mol.L-1
- dans une solution où pH = 4 on a une concentration
[H3O+] = 10 -4/1
[H3O+] = 10-4 mol.L-1
dans une solution où pH = 5,6 on a une concentration
[H3O+] = 10 -5,6/1
[H3O+] = 10-5,6 mol.L-1
[H3O+] = 3,98.10-5 mol.L-1
Voir aussi le cours sur Le pH et la concentration en ions oxonium
Conductimétrie et loi de Kohlrausch
La conductimétrie
La conductimétrie est l’ensemble des méthodes et techniques permettant de mesurer une conductivité.
Elle repose sur l’utilisation d’un appareil (le conductimètre) permettant une mesure directe de la conductivité d’une solution.
La conductivité d’une solution est une grandeur qui dépend directement de la concentration des espèces ioniques qu’elle contient par conséquent:
La conductimétrie permet de déterminer la concentration des espèces chimiques ioniques dissoutes dans une solution.
Résistance, conductance et conductivité
Une portion de solution est comparable à un conducteur ohmique de résistance “R” qui obéit à la loi d’ohm: U = R x I
Cette portion de solution est également caractérisée par sa conductance notée G, exprimée en Siemens (S) qui est définie comme l’inverse de la résistance:
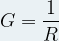
avec G la conductance (S) et R la résistance (Ω)
Cette conductance s’exprime elle-même à partir de la conductivité grâce à la formule suivante :
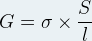
avec G la conductance en Siemens, σ la conductivité en Siemens par mètre, S la surface d’une des plaques utilisées comme électrodes dans la cellule de mesure du conductimètre en mètre carré et “l” la distance entre les deux plaques de la cellule de mesure du conductimètre.
La conductance et la conductivité reflètent la faculté d’une solution aqueuse à conduire le courant: plus elles sont élevées et plus l’intensité du courant l’est aussi .
Cependant la conductance dépend des conditions de mesures (dimension et éloignement des électrodes de la cellule de mesure du conductimètre) alors que la conductivité est propre à la solution (elle ne dépend que de la nature des espèces chimiques dissoutes et de leur concentration).
Conductivité et concentration: la loi de Kolhrausch
La loi de Kolhlrausch permet d’exprimer la conductivité d’une solution en fonction d’une grandeur propre aux ions dissous: leur conductivité molaire ionique.
La conductivité molaire ionique d’un ion se note λ et s’exprime en Siemens mètre carré par mole (S.m2.mol-1)
Expression de la loi de Kolhlrausch:
σ = λ(X1).[X1] + λ(X2).[X2] …. + λ(Xn).[Xn]
où la conductivité (σ) est en siemens par mètre, les conductivités ioniques des ions de la solution ( λ(X1), λ(X2)… λ(Xn) sont en Siemens mètre carré par mole (S.m2.mol-1) et les concentrations molaires [X1], [X2]… [Xn] en mol par mètre cube (mol.m-3)
Exemple, détermination des concentrations dans une solution de sulfate de sodium
Cette solution, obtenue par dissolution de sulfate de sodium Na2SO4, contient des ions sulfate (SO42-) et des ions sodium Na+.
L’équation de dissolution du sulfate de sodium est la suivante:
Na2SO4(s) → SO42-(aq) + 2 Na+(aq)
Par conséquent la concentration en ion sodium est deux fois plus élevée que celle en ion sulfate:
[Na+] = 2 [SO42-]
Dans cette solution, l’utilisation de loi de Kolhraush permet d’obtenir la relation suivante:
σ = λ(Na+).[Na+] + λ(SO42-).[SO42-]
Si les conductivités molaires ioniques sont connues et qu’une mesure permet de déterminer la conductivité de la solution alors on peut exprimer soit la concentration en ion sodium soit celle en ions sulfate.
concentration en ions sulfate:
σ = λ(Na+).[Na+] + λ(SO42-).[SO42-]
σ = λ(Na+).2[SO42-] + λ(SO42-).[SO42-]
σ = [SO42-] x (2 λ(Na+)+ λ(SO42-))^
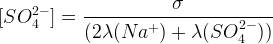
concentration en ions sulfate:
[Na+] = 2 [SO42-]
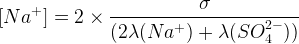
Spectroscopie UV-visible et loi de Beer-Lambert
Principe de la spectroscopie UV-Visible
Un échantillon de solution contenant, sous forme dissoute, l’espèce chimique à analyser est versé dans une cuve qui est elle-même placée dans un spectroscope. Celui-ci soumet la cuve et sa solution à un rayonnement dont la longueur d’onde appartient au domaine UV-visible (longueur d’onde allant environ de 100 nm à 800 nm)
Une partie de ce rayonnement est absorbé en provoquant des transitions énergétiques chez les électrons impliqués dans les liaisons chimiques.
Pour une longueur d’onde donnée (λ) l’intensité du rayonnement incident (I0) et celle du rayonnement transmis (I) permettent d’exprimer l’absorbance (A) à partir de la relation:
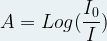
où Les deux intensités sont exprimées dans la même unité et l’absorbance “A” n’a pas d’unité.
Un spectre UV-visible représente l’évolution de la l’absorbance en fonction de la longueur d’onde
Comment identifier une espèce chimique ?
Chaque espèce chimique possède son propre spectre UV-Visible, il est donc possible d’identifier une espèce chimique en comparant son spectre UV-visible à celui d’espèces chimiques connues
Si deux spectres sont identiques (à l’amplitude près) alors ils appartiennent à la même espèce chimique.
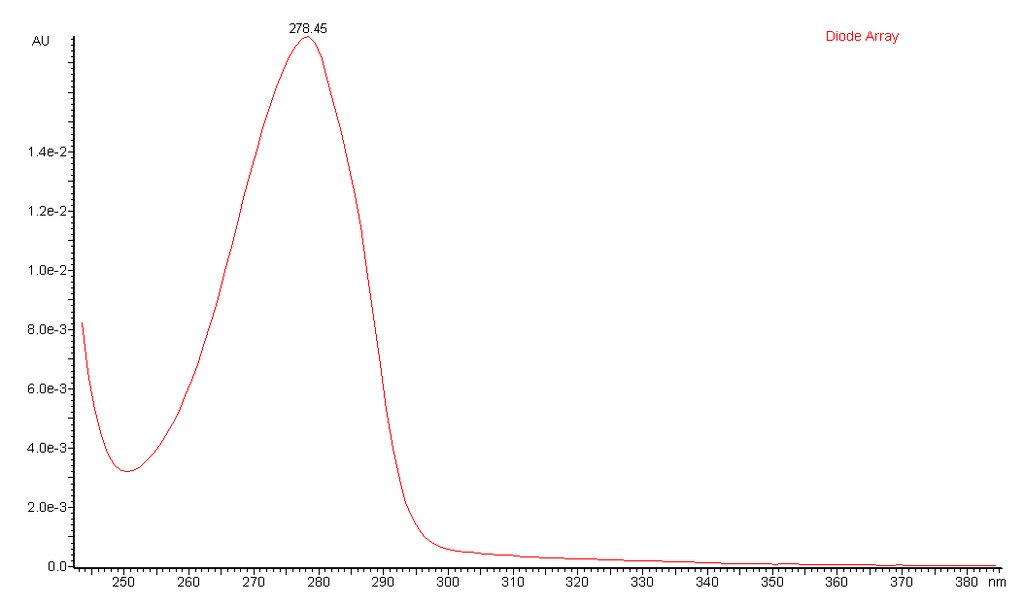
Par ailleurs le spectre UV-visible d’une espèce chimique présente toujours une longueur d’onde (notée λmax) où l’absorbance est maximale. Il s’agit également d’une grandeur qui peut aussi être utilisée pour identifier une espèce chimique.
Exemple : spectre UV de la catechine.
Loi de Beer-Lambert et concentration
La spectroscopie UV-visible permet non seulement d’identifier une espèce chimique mail il est aussi possible de l’exploiter pour déterminer une concentration, en effet l’absorbance, mesurée en spectroscopie UV-visible, est une grandeur qui dépend de la concentration. Cette relation entre absorbance et concentration est donnée par la loi de Beer-Lambert.
Pour une solution comportant uniquement comme soluté l’espèce chimique X1 de concentration [X1], dans une cuve d’épaisseur « l », l’absorbance est donnée par la formule :
Aλ = ελ( X1) x l x [X1]
où :
- « Aλ » est l’absorbance (sans unité) de la solution à la longueur d’onde λ
- « ελ( X1) » est le coefficient d’absorption molaire de l’espèce chimique X1 à la longueur d’onde λ exprimé en litre par mole et par centimètre (L.mol-1.cm-1)
- « l » est l’épaisseur de la cuve en centimètre (cm)
Dans le cas où une solution comporte plusieurs espèces chimiques les absorbances s’additionnent.
Pour deux espèces chimiques :
Aλ = ελ( X1) x l x [X1] + ελ( X2) x l x [X2]
Pour trois espèces chimiques :
Aλ = ελ( X1) x l x [X1] + ελ( X2) x l x [X2] + ελ( X3) x l x [X3]
etc.
Si l’on mesure l’absorbance « A » d’une solution et que le coefficient d’absorption ελ( X1) de l’unique espèce chimique dissoute est connu (il peut être déterminé à partir d’une mesure d’absorbance sur une solution de concentration connue on a alors ελ( X1) = Aλ / (l x [X1] ) on peut déterminer la concentration :
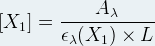
Voir aussi cours sur la loi de Beer-Lambert:
Spectroscopie infrarouge (IR)
Principe
Tout comme la spectroscopie UV-visible, la spectroscopie IR consiste à exposer un échantillon de l’espèce chimique à analyser à un rayonnement qui sera en partie absorbé par cette espèce chimique.
Dans le cas de la spectroscope IR le rayonnement appartient au domaine des infrarouges avec des longueurs d’onde pouvant aller d’environ 2500 nm à 25000 nm
L’énergie absorbée alimente des mouvements de vibration et d’élongation des liaisons au seins des liaisons chimiques de l’espèce chimique analysée.
Un spectre infrarouge est obtenu en représentant la transmittance en fonction du nombre d’onde du rayonnement.
La transmittance (souvent notée T) est une grandeur sans unité qui est définie comme le rapport de l’intensité du rayonnement transmis (I) divisée par l’intensité du rayonnement incident (I0)
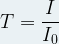
La transmittance peut aussi être exprimée sous forme de pourcentage, dans ce cas son expression devient :
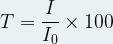
Le nombre d’onde est quant à lui noté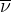 
et correspond à l’inverse de la longueur d’onde exprimée en centimètre, son unité est donc le centimètre moins un (cm-1) :
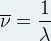
avec λ en centimètre et 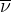en centimètre moins un.
Exemple du spectre infrarouge de l’éthanol
Utiliser un spectre infrarouge pour identifier les constituants d’une espèce chimique
Un spectre infrarouge comportement des pics plus ou moins larges et plus ou moins intenses situés sur des intervalles de nombres d’onde qui dépendent de la nature des groupements d’atomes présents dans l’espèce chimique.
Un spectre infrarouge permet d’identifier les groupes caractéristiques présents dans une espèce chimique mais il ne permet pas nécessairement d’identifier cette espèce chimique.
Voir cours de première spécialité « Comment identifier une espèce chimique avec la spectroscopie IR »
Principales bandes d’absorptions infrarouge
| Liaison | Particularité | Plage d’absorption (nombre d’onde en cm-1) |
| C–H | Bande de largeur variable d’intensité moyenne à forte de 2850 cm–1 à 3000 cm–1 | |
| O–H | Avec liaison hydrogène (ce qui inclut les solutions aqueuses) | Bande large et forte de 3200 cm–1 à 3600 cm–1 |
| O–H | Groupe carboxyle | Bande large forte, moyenne à large 2 500 cm–1 à 3 500 cm–1 |
| C=O | Cétone ( le carbone n’est lié à aucun hydrogène) | Bande fine et forte vers 1715 cm–1 |
| C=O | Aldéhyde (Le carbone est lié à un hydrogène) | Bande fine de faible à moyenne intensité entre 2700 et 2830 cm–1 (deux pics) |
| C=O | Acide carboxylique | Bande fine de forte intensité vers 1715 cm-1 |
| N-H | Amine primaire (une seule liaison azote-carbone) | Bande large d’intensité moyenne à forte entre 3300 et 3500 cm-1 |
Dosage par étalonnage
Définition
Un dosage par étalonnage consiste à déterminer la concentration d’une solution en comparant l’une de ses caractéristiques physiques à celle de solutions (dites solutions étalons).
Principe
Le dosage par étalonnage repose sur la mesure d’une grandeur physique : la masse volumique, la densité, l’absorbance, la conductivité.
Cette grandeur doit pouvoir être mesurée d’une part pour la solution de concentration inconnue et d’autre part pour les solutions étalons.
Les solutions étalons constituent une « gamme » de solutions, leurs concentrations doivent couvrir un intervalle le plus large possible permettant d’inclure la valeur de concentration inconnue.
En générale les solutions étalons sont préparées à partir d’une solution mère (suffisamment concentrée) à laquelle on fait subir une série de dilutions.
On peut par exemple utiliser :
- une solution S0 de concentration C0 = 10-1 mol.L-1
- on dilue S0 d’un facteur 10 de manière à obtenir une solution S1 de concentration C1 = 10-2 mol.L-1.
- Cette solution S1 est ensuite elle-même diluée d’un facteur 10 pour obtenir une solution S2 de concentration C2 = 10-3 mol.L-1.
- Cette solution S2 est ensuite elle-même diluée d’un facteur 10 pour obtenir une solution S3 de concentration C2 = 10-4 mol.L-1.
Etc, en général on de ne va pas au-delà d’une concentration à 10-6 mol.L-1.
Déterminer la concentration inconnue
Le dosage par étalonnage peut se limiter à fournir un encadrement de la concentration inconnue en repérant les solutions qui encadrent la solution inconnue
Si par exemple :
- une solution de concentration « C » inconnue possède une absorbance A = 0,66
- une solution étalon S3 a une concentration C3 = 5,00.10-3 mol.L-1 et une absorbance A3 = 0,70
- une solution étalon S4 a une concentration C4 = 1,00.10-3 mol.L-1 et une d’absorbance A4 = 0,14
Puisque A4 < A < A3 alors C4 < C < C3
Etant donné que l’absorbance de la solution de concentration inconnue est comprise entre celle de la solution étalon S4 et celle de la solution étalon S3 alors on peut en déduire que sa concentration est également comprise entre la concentration de la solution étalon S4 et celle de la solution étalon S3.
Donc 1,00.10-3 < C < 5,00.10-3
Le tracer d’une courbe d’étalonnage permet d’extrapoler la valeur de la concentration inconnue.
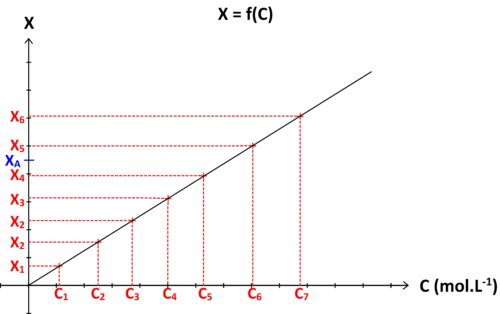
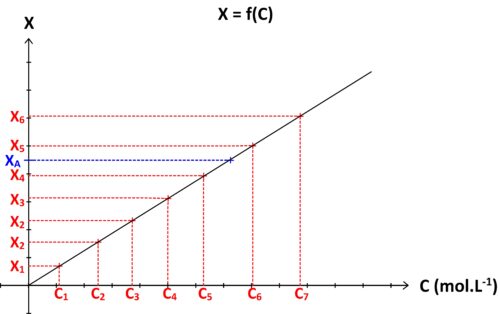
Si l’on réalise une gamme de solutions étalons S1, S2, S3….Sn , de concentrations respectives C1, C2, C3 … Cn caractérisées chacune par une grandeur physique « X » de valeur X1, X2, X3 … Xn, alors il est possible de tracer une courbe d’étalonnage représentant la grandeur physique étudiée « X » en fonction de la concentration : X = f (C)
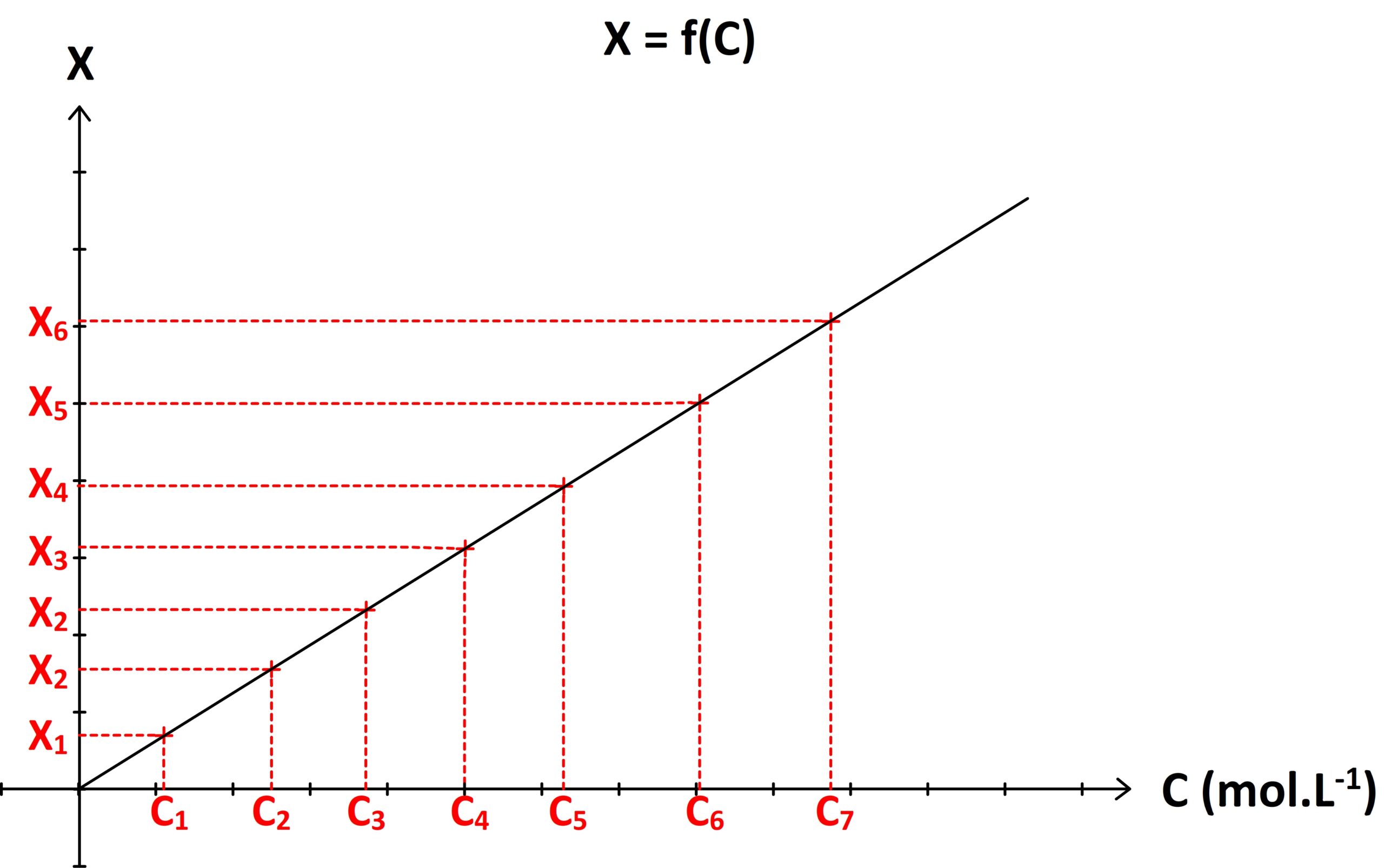
Si la solution à doser est caractérisée par une concentration inconnue CA et une valeur de grandeur physique mesurée XA alors alors :
- on repère sur graphe l’ordonnée de valeur XA
- on détermine le point de la courbe d’étalonnage possédant cette ordonnée
- on détermine l’abscisse de ce point
L’abscisse ainsi déterminée graphiquement correspond à la concentration CA recherchée
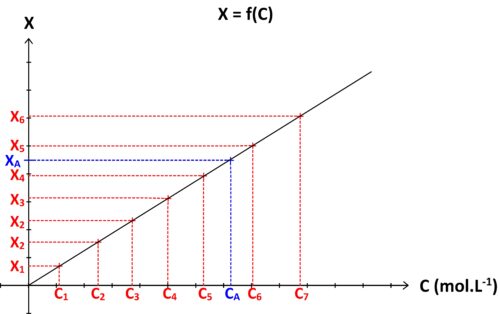
Dans le cas où la grandeur physique étudiée (comme l’absorbance où la conductivité) est proportionnelle à la concentration alors il est possible de prolonger la courbe d’étalonnage dans la limite de validité de la relation entre grandeur physique et concentration.
Déterminer la quantité de matière d’un gaz
L’équation d’état d’un gaz parfait est une relation entre la température, la pression, le volume et la quantité de matière :
P.V = n .R.T
Elle permet donc d’exprimer la quantité de matière :
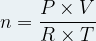
où :
- P est la pression du gaz en Pascal
- V est le volume du gaz en mètre cube
- R est la constante des gaz parfait (R = 8,314 J.mol-1.K-1)
- T est la pression en Kelvin
La quantité de matière d’un gaz peut donc être déterminée à condition de connaître son volume, sa température et sa pression.
L’équation d’état des gaz parfaits permet aussi d’exprimer le volume d’un gaz.
Par définition, le volume molaire d’un gaz correspond au rapport de son volume par sa quantité de matière :
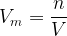
D’après l’équation d’état du gaz parfait :
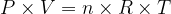
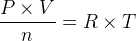
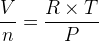
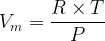
L’expression du volume molaire d’un gaz parfait ne dépend que de la température et de la pression mais pas de la nature chimique du gaz : si la pression et la température sont les mêmes alors le volume molaire a même valeur pour du dioxyde de carbone, du diazote ou par exemple du méthane.
D’après cette relation le volume molaire d’un gaz est: