Constitution et transformations de la matière – 2. Modéliser l’évolution temporelle d’un système, siège d’une transformation – B) Modéliser l’évolution temporelle d’un système, siège d’une transformation nucléaire
- Stabilité des noyaux
- Lois de conservation
- Radioactivités α, β, et γ
- Loi de décroissance radioactive
- Application de la radioactivité naturelle à la datation
- Autres applications de la radioactivité

Stabilité des noyaux
Un noyau est dit instable s’il est radioactif, il est alors susceptible de se désintégrer, c’est à dire se transformer spontanément en un autre noyau appelée « noyau fils »
Au contraire un noyau est dit stable s’il ne subit spontanément aucune transformation nucléaire.
Il est possible de visualiser éléments stables et instables grâce à un diagramme (N,Z), aussi appelé diagramme de Segré. Son axe des ordonnées correspond à N (nombre de neutrons) et son axe des abscisses correspond à Z (numéro atomique, nombre de protons)
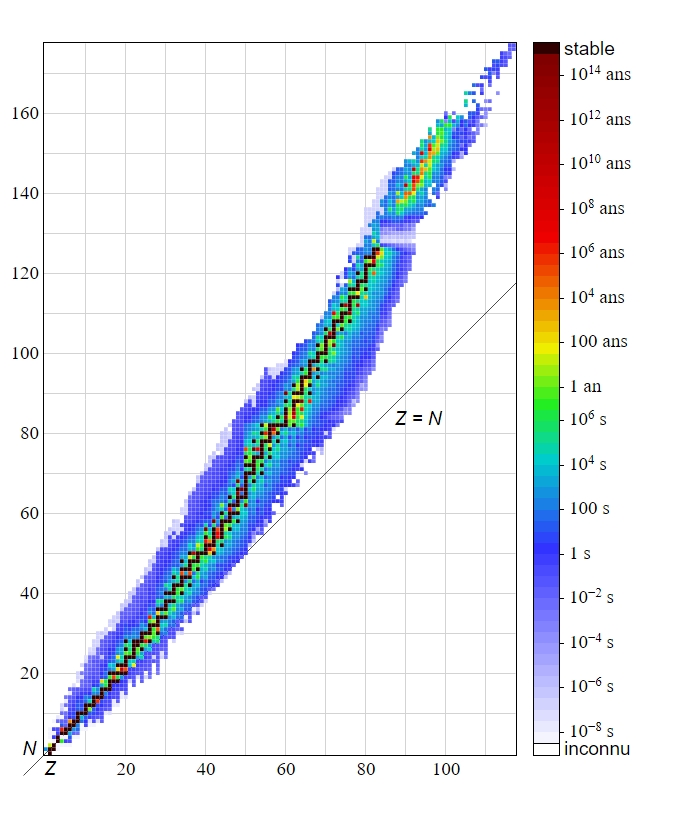
La zone de stabilité (en noir sur le diagramme précédent) est tangente à la courbe d’équation N = Z pour les faibles valeurs de Z mais s’en éloigne progressivement au fur et à mesure que « Z » augmente.
D’après ce diagramme on peut distinguer trois zones d’instabilité :
- Au-delà d’une certaine d’une certaine limite (Z=83) les éléments ne disposent plus d’isotopes stable, la radioactivité est alors le plus souvent de type α
- Au dessous de la zone de stabilité les isotopes instables présentent un excès de protons par rapports aux neutron et présentent une radioactivité β+.
- Au dessous de la zone de stabilité les isotopes instables présentent un excès de neutrons par rapport aux proton et présentent une radioactivité β–.
Lois de conservation
Lors d’une transformation radioactive les noyaux et particules qui interviennent suivent des lois de conservation (appelées lois de Soddy), elles permettent d’écrire des équations de réaction nucléaire équilibrées :
- Conservation de la charge électrique
La charge électrique est notée « Z », elle est exprimée en nombre de charges élémentaires et peut être soit positive soit négative.
Sa conservation implique que :
La charge totales des particules réactive est égale à la charge totale des particules produites
- Conservation du nombre de nucléons
Le nombre de nucléons est indiqué par le nombre de masse « A »
Sa conservation implique que :
Le nombre totale de nucléons pour les réactifs correspond au nombre total de nucléons pour les produits.
Si l’on prend le cas d’une désintégration radioactive au cours de laquelle un noyau père X1 forme un noyau fils X2 en produisant un nombre « n » de particules « A3 » suivant l’ une équation suivante :
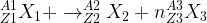
D’après la loi de conservation de la charge électrique : Z1 = Z2 + n.Z3
D’après la loi de conservation des nucléons : A1 = A2 + n.A3
Radioactivités α, β, et γ
- La radioactivité α
Elle concerne principalement les noyaux « lourd » (dont le numéro atomique est proche de 100).
La désintégration α se caractérise par l’émission d’une particule α (des noyau d’hélium 4)
L’équation de désintégration est de la forme suivante :
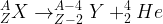
La radioactivité β+
Elle concerne principalement les noyaux présentant un excès de protons (sous la zone de stabilité du diagramme N,Z)
La désintégration β+ se caractérise par l’émission d’un positon (particule d’antimatière correspondant à un anti-électron) et une équation de la forme suivante :

- La radioactivité β–
Elle concerne principalement les noyaux présentant un excès de neutrons (au-dessus la zone de stabilité du diagramme N,Z)
La désintégration β– se caractérise par l’émission d’un électron et une équation de la forme suivante :
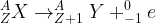
- La radioactivité γ
Lors d’une désintégration α, β+ ou β– , le noyau fils produit se trouve dans un état dit excité noté Y*, c’est à dire dans un état d’énergie supérieur à son état fondamental. Il se désexcite en émettant un rayonnement qui appartient dans la majorité des cas au domaine des rayons gamma.
On peut traduire cette désexcitation par l’équation :
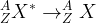
Loi de décroissance radioactive
Le nombre de noyaux radioactifs dans un échantillon de matière est appelé « population de noyau », il est noté «N »
L’activité (A) d’une population de noyaux radioactifs est définie comme l’opposé de la dérivée de cette population par rapport au temps :
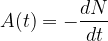
L’activité correspond à un nombre de désintégrations par seconde mais elle s’exprime en Becquerel (Bq).
Par ailleurs l’activité d’une population de noyaux radioactifs est également proportionnelle au nombre de noyaux « N » de cette population :
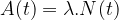
où :
- A(t) est l’activité en becquerel (Bq)
- N(t) est le nombre de noyaux
- λ est la constante radioactive (en s-1) caractéristique de l’isotope auquel correspondent les noyaux de la population étudiée
Il résulte des deux expressions précédente de l’activité l’équation différentielle suivante :
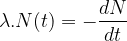
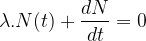
Cette équation différentielle admet la solution suivante
N(t) = N0.exp (-λ.t)
où
- N(t) est le nombre de noyau à l’instant « t »
- N0 est le nombre initial de noyaux (nombre de noyaux à l’instant t = 0)
- λ est la constante radioactive (en s-1) de l’isotope
- t est le temps en seconde
Rappel : le temps de demi-vie (t1/2) d’un isotope correspond à la durée au bout de laquelle la population de cet isotope est divisée par deux.
Par conséquent :
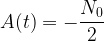
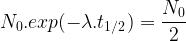
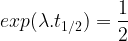
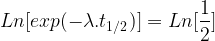

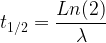
et
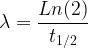
Voir aussi la la partie consacrée à la demi-vie dans le cours d’enseignement scientifique de première « Niveau d’organisation des éléments chimiques » https://webphysique.fr/niveau-organisation-elements-chimiques/#demi-vie
Application de la radioactivité naturelle à la datation
D’après la loi de décroissance radioactive il est possible d’exprimer le nombre de noyaux grâce à la relation suivante :
N(t) = N0.exp (- λ.t)
Il est aussi possible d’exprimer le temps en fonction du nombre de noyaux :
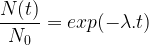
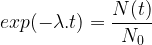
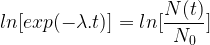
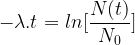
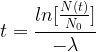
Soit la relation :
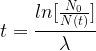
On au peut aussi exprimer le temps écoulé en fonction de la demi-vie au lieu de la constante radioactive
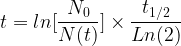
La datation n’est possible que si le nombre de noyaux constituant la population initial est connu
Pour que cette datation puisse se faire avec une précision suffisante il est également nécessaire que la durée à déterminer ne soit pas trop faible par rapport à la demi-vie.
Autres applications de la radioactivité
- La tomographie est une technique exploitant la radioactivité β+
- La scintigraphie exploite la radioactivité
