Enseignement scientifique de première – Partie 4 – Son et musique, porteurs d’information – 4.1 – Le son, phénomène vibratoire
- Qu’est-ce qu’un son ?
- Les sons purs
- Fréquences des sons purs audibles
- Les sons composés
- Fréquence fondamentale
- Harmoniques d’un son composé
- Spectre d’un son
- Son produit par un instrument
- Intensité sonore
- Niveau d’intensité sonore
- Seuils d’audibilité, de danger et de douleur
- Son produit par une corde vibrante
Qu’est-ce qu’un son ?
Un son est une onde mécanique qui consiste en une variation périodique de pression se propageant dans un milieu matériel (air, eau, verre…)
Les couches d’air oscillent lorsqu’elles transmettent un son ( elles s’écartent temporairement de leur position initiale avant d’y revenir) mais globalement il n’y a pas de transport de matière.
Par contre la propagation d’un son s’accompagne d’une propagation d’énergie (celle de la source qui l’a produit).
Nous pouvons entendre un son grâce à notre système auditif : le tympan capte les sons (il détecte les variations périodiques de pression) et les transmet à l’oreille interne où le cellules ciliées les convertissent en signal nerveux transmis au cerveau.
Pour une description plus détaillée de la nature d’un son voir cours de seconde «Emission et perception d’un son »
Les sons purs
Définition
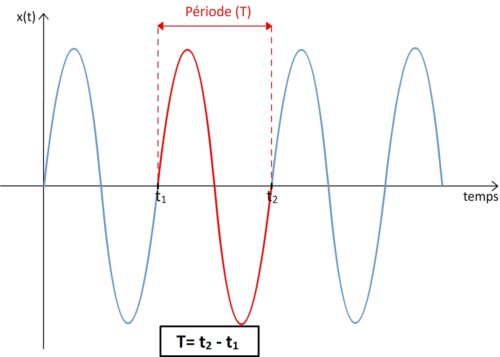
On peut de qualifier de « pur » un son caractérisé par une seule fréquence « f » et une seule période « T ».
Si un son est pur alors son amplitude obéit à une loi « sinusoïdale »
L’enregistrement d’un tel son donne une courbe caractéristique (exprimable à l’aide d’une fonction mathématique « sinus ») constituée d’une succession de « vagues » positives (au-dessus de l’axe horizontal du temps) et de vagues négatives (au-dessous de l’axe horizontal) de durées toutes identiques
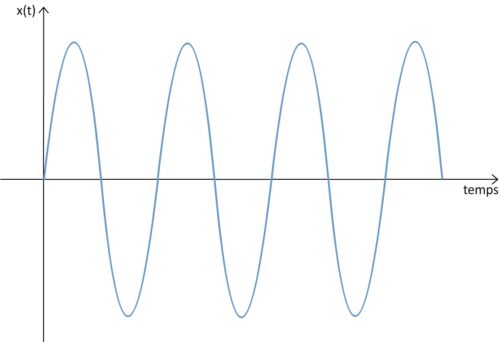
Une oscillation correspond à un motif élémentaire qui associe une « vague » positive et une « vague » négative.
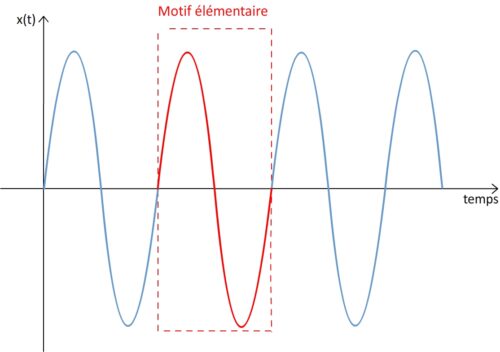
La durée du motif élémentaire correspond à la période « T » du son pur.
La période d’un son pur peut donc être déterminée à partir de l’enregistrement d’un son en déterminant la durée d’une oscillation.
La fréquence « f » d’un son pur correspond au nombre de vibration par seconde, on peut l’exprimer comme l’inverse de la période grâce à la formule suivante :
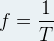
où :
Par exemple :
Inversement cette relation peut être modifiée pour permettre de déterminer la valeur de la période à partir de la fréquence :
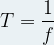
Fréquences des sons purs audibles
Le système auditif humain a ses limites, il ne permet de percevoir que des sons dont la fréquence est comprise dans un intervalle limité.
En général on peut faire l’approximation que les sons audibles ont une fréquence allant de 20 Hz à 20 000 Hz
- Les sons de fréquence inférieure à 20 Hz sont appelés « infrasons »
- Les sons de fréquence supérieure à 20 000 Hz sont appelés « ultrasons »

Un son pur peut être par exemple produit par un diapason ou par une enceinte.
Les sons composés
Un son est dit composé (ou complexe) s’il est caractérisés par plusieurs fréquences (et donc aussi plusieurs périodes) de vibration.
Un son composé peut être considéré comme l’addition de plusieurs sons pur.
Si l’on compare le domaine du son à celui de la lumière alors le son pur est l’analogue d’une lumière monochromatique tandis qu’un son composé est l’analogue d’une lumière polychromatique.
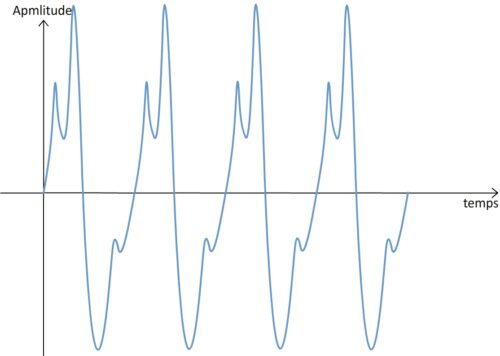
L’enregistrement d’un son composé donne une courbe toujours périodique mais qui n’est plus sinusoïdale.
Fréquence fondamentale
Définition
La fréquence fondamentale d’un son composé correspond à la plus petite fréquence de vibration qui le caractérise. On la note souvent f0.
Sur le graphique d’un enregistrement sonore la fréquence fondamentale est celle associée au motif élémentaire.
Harmoniques d’un son composé
Définition
Les harmoniques sont les fréquences caractéristiques des vibrations d’un son composés dont les valeurs sont supérieures à celle de la fréquence fondamentale.
Chaque harmonique possède une valeur qui est un multiple entier de la fréquence fondamentale
La première harmonique a une fréquence f1 = 2 x f0
La deuxième harmonique a une fréquence f2 = 3 x f0
La troisième harmonique a une fréquence f3 = 4 x f0
La quatrième harmonique a une fréquence f4 = 5 x f0
etc
Par exemple un son composé de fréquence fondamentale f0 = 220 Hz a des harmoniques de fréquences 440 Hz, 660 Hz, 880 Hz, 1100 Hz….
Spectre d’un son
Définition
Le spectre d’un son est un graphique indiquant sa fréquence fondamentale ainsi celles de ses harmoniques en précisant leurs amplitudes relatives.
Le spectre est donc un graphique :
- dont l’axe abscisses indique des fréquences (en Hz)
- dont l’axe des ordonnées peut indiquer une amplitude, une intensité sonore, un niveau d’intensité, un pourcentage..
- comportant une barre verticale pour chaque fréquence (fondamentale ou harmonique)
Le spectre d’un son composé aura la forme suivante :
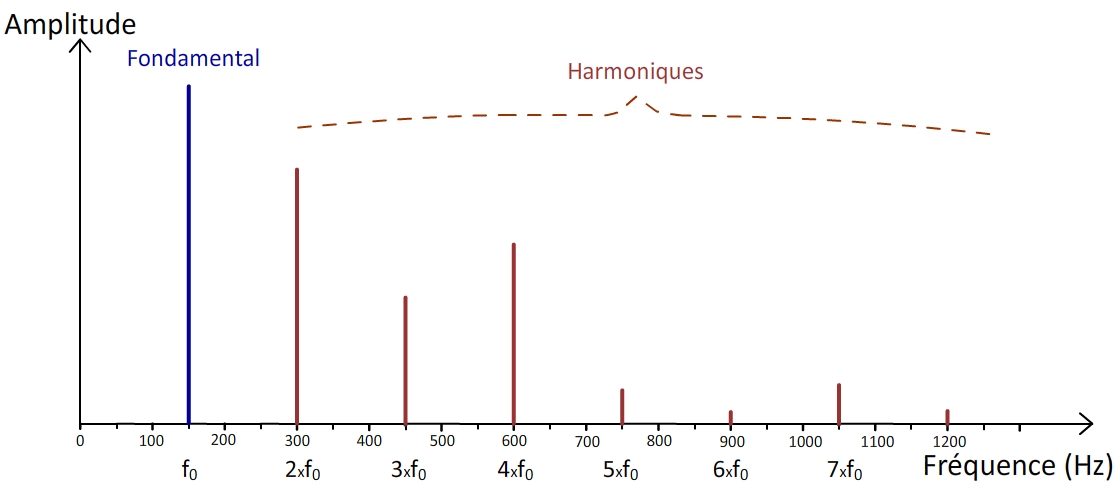
La fréquence la plus faible correspond à la fréquence fondamentale f0
Les autres fréquences sont celles des harmoniques, elles sont des multiples de la fréquence fondamentale.
Le spectre d’un son pur aura toujours l’aspect suivant :
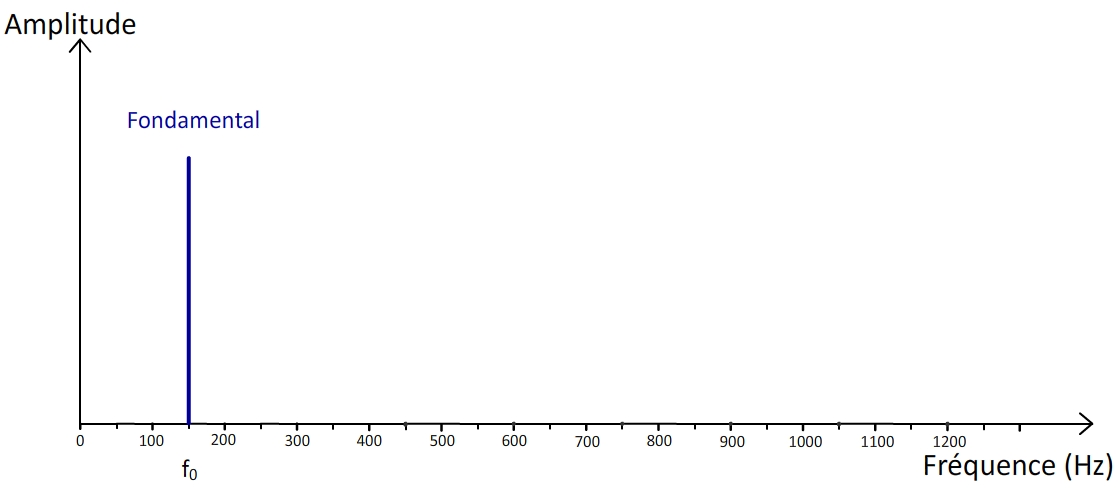
Il ne comporte (par définition) toujours qu’une seule fréquence.
Son produit par un instrument
Richesse d’un son : les instruments de musiques produisent tous des sons composés qui sont perçus comme d’autant plus « riches » que le nombre des harmoniques est important.
Le timbre : chaque instrument se caractérise par son timbre qui dépend du nombre et de l’amplitude relative des harmoniques.
En raison du timbre propre à chaque instrument musical la même note jouée par deux instruments différents est perçue de manière différente :
- Les spectres de cette note sont différents, ils comportent la même fréquence fondamentale et les mêmes fréquences harmoniques mais les amplitudes relatives sont différentes.
- Les enregistrements de ces notes comportent des motifs de même période mais de formes différentes.
Intensité sonore
L’intensité sonore est une grandeur notée I (comme Intensité) qui s’exprime en watt par mètre carré (W.m-2).
Elle traduit la puissance transmise par un son : plus l’intensité sonore est élevée et plus le son est « fort ».
L’intensité sonore est proportionnelle à la puissance de la source sonore.
Une source de puissance deux fois plus élevée permet de produire un son d’intensité deux fois plus élevée, une source de puissance dix fois plus élevée permet de produire un son d’intensité dix fois plus élevée etc.
C’est une grandeur additive.
Si un point de l’espace reçoit un son d’intensité I1 et un son d’intensité I2 alors l’intensité sonore totale est Itot = I1 + I2
Si un point de l’espace reçoit des sons d’intensité I1, I2, I3 alors l’intensité sonore totale est Itot = I1 + I2 + I3
etc
Plus la distance par rapport à la source sonore est élevée et plus l’intensité sonore est faible
Si une source sonore diffuse sa puissance (P) dans toutes les directions de l’espace alors un point situé à une distance « d » de cette source reçoit un son d’intensité I tel que :
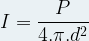
D’après cette relation l’intensité sonore est inversement proportionnelle au carré de la distance à la source : si la distance est multipliée par « 2 » alors l’intensité est divisée par 22 = 4, si la distance est multipliée par 3 alors l’intensité et divisée par 32= 9 etc
Il n’est pas possible de percevoir des sons dont l’intensité est inférieure à la valeur I0 = 10-12 W.m-2
La valeur I0 = 10-12 W.m-2 constitue le seuil d’audibilité
Niveau d’intensité sonore
L’intensité sonore prend des valeurs dont les ordres de grandeurs très différents (de 10-12 W.m-2 à environ 1 W.m-2), c’est en partie pour éviter cet inconvénient qu’a été définie une autre grandeur : le niveau d’intensité sonore.
Le niveau d’intensité sonore se note « L » et a pour unité le « Bel » de symbole B, néanmoins il est presque systématiquement exprimé a l’aide d’une de ses unités dérivées : le décibel de symbole dB.
Tout comme l’intensité sonore (qui sert à le définir) le niveau d’intensité sonore traduit la « force » avec laquelle est perçue un son.
Le niveau d’intensité sonore est défini par la formule suivante :
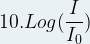
où :
- I est l’intensité sonore du son en watt par mètre carré (W.m-2)
- I0 est le seuil d’audibilité (I0 = 10-12 W.m-2 )
- L est niveau d’intensité sonore en décibel (dB)
Cette formule fait intervenir la fonction mathématique logarithme décimal (à ne pas confondre avec la fonction logarithme népérien), elle correspond à la fonction réciproque de la fonction puissance de 10. Voici quelques unes de ces propriétés pouvant être utiles.
Log (xa) = a x Log (x)
Exemples
- Log (26) = 6 x Log (2)
- Log (102) = 2 x Log (10)
Si Log (x) = a alors x = 10a
Exemples
si log (x) = 6 alors x = 106
si log (x) = -10 alors x = 10-10
Log (a x b) = Log (a) + Log (b)
Exemples
Log (2 x a) = Log (2) + Log (a)
Log (10 x 5) = Log(10) + Log (5)
Il est également possible de déterminer l’intensité sonore à partir du niveau d’intensité :
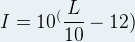
Seuils d’audibilité, de danger et de douleur
Le seuil d’audibilité
Définition
Le seuil d’audibilité correspond à la plus faible intensité sonore pour laquelle un son peut être entendu.
On admet comme valeur du seuil d’audibilité I0 = 10-12 W.m-2
Il correspond à un niveau d’intensité sonore L = 0
Le seuil de douleur
Définition
Le seuil de douleur correspond à la valeur d’intensité sonore à partir de laquelle le son provoque une douleur.
La valeur généralement attribuée au seuil de douleur est une intensité sonore d’un watt.
Seuil de douleur, intensité sonore I = 1 W.m-2
Elle correspond à un niveau d’intensité sonore que l’on peut déterminer grâce à la formule liant ces deux grandeurs :
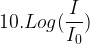
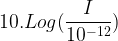
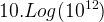
L = 10 x 12
L = 120 dB
Seuil de douleur, niveau d’intensité sonore L = 120 dB
Son produit par une corde vibrante
Les instruments à corde (guitare, harpe, piano, violon) produisent des sons grâce à la vibrations de cordes.
La fréquence du son produit par une corde dépend de trois facteurs : sa longueur, sa masse linéique et la tension exercée sur cette corde.
La longueur de la corde
Elle correspond à la distance qui sépare les deux extrémités fixes de la corde.
Plus cette cette longueur élevée plus le rythme des vibrations est lent ce qui correspond à une diminution de fréquence. Pour être plus précis la fréquence de vibration est inversement proportionnelle à la longueur de la corde :
- Si une corde est deux fois plus longue qu’une autre (et que les autres caractéristiques sont identiques) alors la fréquence est deux fois plus faible.
- Si une première corde a une longueur trois fois plus élevée qu’une seconde alors la première corde à une fréquence de vibration trois fois plus faible que la seconde
etc
Lorsque la longueur de vibration d’une corde augment sa fréquence diminue
La masse linéique
La masse linéique (ou masse linéaire) souvent note μ (lettre grecque micro) correspond à la masse d’un corps linéaire par une unité de longueur.
Si une corde a une masse « m » et une longueur « L » alors sa masse linéique est :
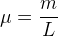
avec μ en kilogramme par mètre (kg.m-1), m en kilogramme (kg) et L en mètre (m).
Si par exemple une corde de longueur 82 cm a une masse de 56 g alors sa masse linéique a pour valeur :
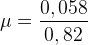
μ = 0,056 / 0,82
μ =0,068 kg.m-1
Plus la corde est « lourde » et plus sa vibration est lente par conséquent :
Plus la masse linéique d’une corde est élevée et plus la fréquence de vibration est faible.
Tension exercée sur la corde
Elle correspond à la force exercée sur la corde pour la tendre, on la note souvent « T » et elle s’exprime en Newton (comme toutes les forces).
Plus cette tension est important et plus la vibration de la corde est rapide, par conséquent :
Plus la tension exercée par sur la corde est importante et plus sa fréquence de vibration est élevée.
A réviser avant d’aborder ce cours
Cours de seconde:
Fiche de cours:

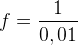 = 100 Hz
= 100 Hz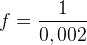 = 500 Hz
= 500 Hz