Modéliser une action sur un système

Cours de physique niveau seconde – Mouvement et interaction

• Qu’est-ce qu’une action ?
• Les forces
• Principe des actions réciproques
• Actions de contact et actions à distance
• Interaction gravitationnelle
• Le poids
• Force exercée par un support
• Force exercée par un fil
• Exercices corrigés pour s’entrainer

Voir aussi la version vidéo de ce cours

Qu’est-ce qu’une action ?

Définition d’une action:

Il y a une action lorsqu’un système agit sur un autre système

La notion d’action est très large, il peut s’agir par exemple:

• D’une main soulevant un sac
• D’ une raquette renvoyant une balle
• D’un satellite tournant autour de la Terre en raison de l’attraction gravitationnelle
• D’une aiguille de boussole qui s’oriente vers le nord sous l’effet du champ magnétique créé par le noyau métallique de la Terre.

Lors d’une action il y a toujours:

• Un système qui exerce l’action (l’auteur)
• Un sytème qui subit l’action (la cible de l’action, le receveur)

Par exemple:

• lorsqu’un lycéen soulève son cartable, le lycéen est l’auteur de l’action tandis que son cartable est la cible de cette action.
• lorsqu’un aimant attire un morceau de fer, l’aimant (l’auteur) agit sur le morceau de fer (la cible).

Voir cours “Les actions mécaniques”

Actions de contact et actions à distance

On distingue deux grandes catégories d’actions: les actions de contact et les actions à distance.

Définition d’une action de contact:

Il y a action de contact lorsque qu’une action ne peut se faire que par un contact entre l’auteur de l’action et la cible.

Exemples:

• une table supporte un livre
• un marteau enfonce un clou
• le vent (l’air en Mouvement) soulève un cerf-volant

Lorsque deux systèmes sont en contact il y a toujours une force de contact qui s’exerce entre ces deux systèmes.

Définition d’une action à distance:

Il y a action à distance si une action peut se faire sans contact entre l’auteur et la cible.

Les actions à distance sont les actions de nature:

• gravitationnelle ( le Soleil attire la Terre, la Terre attire vers elle les objets…)
• électrique ( les corps chargés s’attirent ou se repoussent )
• magnétique ( les aimants s’attirent ou se repoussent enre eux et attirent les corps contenant du fer)
• nucléaire (attraction entre les nucléons)

Voir cours “Les actions mécaniques”

Les forces

Une force modélise l’action d’un système sur un autre.

La notation d’une force est en général de la forme:

F_Auteur/Cible

La lettre “F” (comme force) est la plus utilisée mais elle peut, dans certains cas particuliers, être remplacée par une autre lettre.

En indice on note tout d’abord le nom du système qui exerce la force puis ensuite le nom de celui qui la subit.

Par exemple F_{élève/chaise} désigne la force exercée par l’élève sur une chaise mais la notation F_{chaise/élève} correspond à la force exercée par la chaise sur l’élève.

Elle est caractérisée par:

• un point d’application (point où s’exerce l’action)
• une direction qui (la même que celle de l’action)
• un sens (le même que celui de l’action)
• une intensité qui s’exprime en Newton (N)
• éventuellement la droite d’action (droite ayant la même direction que la force et passant par le point d’application)

Une force peut être représentée par un vecteur force.

Si un système “A” exerce une force sur un système “B” alors cette force peut être représentée par le vecteur:

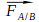
Ce vecteur:

• a pour origine le point d’application de la force
• la même direction que la force
• le même sens que la force
• Une longueur appelée “norme” proportionnelle à la valeur de la force

Voir cours “Les forces ”

Principe des actions réciproques

Ce principe est aussi connu sous le nom de troisième loi de Newton.

Enoncé du principe des actions réciproques:

Toute action d’un système A sur un système B s’accompagne d’une action du système B sur le système A (action réciproque) qui a:

• même direction
• même intensité
• sens opposé

D’après ce principe, à chaque fois qu’un système agit sur un autre système il subit lui-même une action qui est l’opposée de celle qu’il exerce.

Ce principe peut aussi être formulé en terme de forces:

S’il existe une force exercée par un système A sur un système B alors il existe aussi une force exercée par le système B sur le système A telle que :

= –

Puisque chaque action est accompagnée d’une action réciproque on parle souvent d’interaction:

Le terme d’interaction désigne une action et son action réciproque.

Voir cours “Les actions mécaniques”

Interaction gravitationnelle

L’interaction gravitationnelle est l’interaction qui existe systématiquement entre deux systèmes possédant chacun une masse.

La valeur de la force de gravitation qui s’exerce entre un système A et un système B est donnée par la loi universelle de gravitation qui s’exprime par la relation suivante:

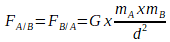
où:

• F_A/B est l’intensité de la force de gravitation en newton (N)
• G est la constante de gravitation universelle de valeur G= 6,67×10^–11 N·m²·kg^-2 = 6,67×10^–11 S.I.
• m_A est la masse du système A en kilogramme (kg)
• m_B est la masse du système B en kilogramme (kg)
• d est la distance qui sépare le centre du système A et le centre du système B en mètre (m)

La force de gravitation possède aussi une expression vectorielle:

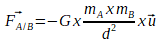
Dans cette expression est un vecteur unitaire (cette à dire un vecteur dont la norme vaut “1”) ayant même direction et même sens que (le vecteur ayant pour origine le point A centre du système A et pour extrémité le point B centre du système B).

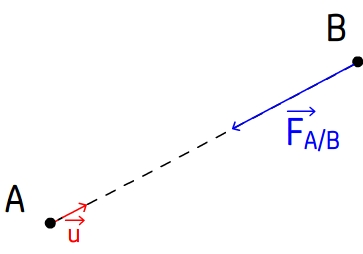
En résumé les caractéristiques de la force de gravitation exercée par un système A sur un système B sont les suivantes:

• Point d’application: le centre du système B (plus précisément le centre de gravité)
• Direction: celle de la droite (AB) joignant les centres des systèmes A et B
• Sens: du système B vers les système A (la force de gravitation est attractive)
• Intensité: donnée par la loi de gravitation universelle

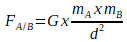
Voir cours:

• “La force de gravitation ”
• “La loi de gravitation universelle ”

Le poids

Définition du poids:

Le poids est la force exercée par un astre sur un corps proche de sa surface, il résulte principalement de la force de gravitation exercée par cet astre.

Le poids se note “P”, le vecteur poids se note et il s’exprime comme toutes les forces en newton (N)

Puisqu’il est une forme de la force de gravitation on peut exprimer sa valeur à l’aide de la loi universelle de gravitation:

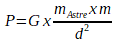
Si le système étudié est à la surface de l’astre alors la distance “d” qui sépare le centre des deux systèmes correspond au rayon R_A de l’astre. Et l’expression devient:

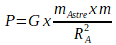
Dans cette expression la partie 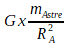correspond à un terme appelé intensité de la pesanteur et on la note “g”

Le poids s’exprime donc à l’aide la relation habituelle:

P = m x g

où

• m est la masse du système en kilogramme (kg)
• g est l’intensité de la pesanteur en newton par kilogramme (N.kg^-1)
• P est le poids du système en newton (N)

“g”, l’intensité de la pesanteur peut donc être calculée grâce à la relation:

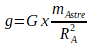
Expression vectorielle du poids:

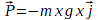
où est un vecteur unitaire vertical.

Voir cours:

• “Le poids, force de pesanteur terrestre ”
• “L’intensité de la pesanteur ”

Force exercée par un support

Définition

Lorsqu’un système repose sur un support alors ce dernier exerce sur le système une force de contact qui le maintient à sa surface.

Caractéristiques:

• Point d’application: centre de la zone de contact.
• Direction: perpendiculaire à la surface de contact en l’absence de frottements et incliné par rapport à la perpendiculaire dans le cas où il y a des frottements.
• Orientation: du support vers l’objet.
• Valeur: égale au poids si le poids est la seule autre force subie par le système.

La force exercée par un support est en général considérée comme la combinaison:

• d’une composante perpendiculaire au support notée
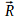
• d’une composante tangente au support qui correspond à une force de frottement notée

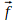
Force exercée par un fil

La force exercée par un fil sur un sytème qui est suspendu a les caractéristiques suivantes:

• Point d’application: point d’attache du fil au système.
• Direction: celle du fil
• Sens: du système vers le fil
• Intensité: variable selon la situation

Cette force est aussi appelée tension du fil et souvent notée