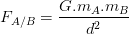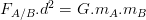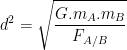La loi de gravitation universelle

1. Présentation
2. Expression mathématique de la loi de gravitation universelle
3. Astuces pour utiliser la loi de gravitation sans erreur
4. Exemple de calcul de la force de gravitation
5. Influence de la masse
6. Influence de la distance
7. Utiliser la loi de gravitation pour calculer une masse
8. Utiliser la loi de gravitation pour calculer une distance

Présentation

La loi de la gravitation universelle correspond à l’expression de la valeur de la force de gravitation s’exerçant entre deux corps. Elle est formulée par Isaac Newton qui la présente dans son ouvrage “Principia mathematica philosophiae naturalis” publié en 1687, elle est le résultat de plusieurs années de travail exploitant, entre autres, de nombreuses données astronomique. Newton n’a pas découvert la gravitation mais il est le premier à faire l’hypothèse que la gravitation terrestre n’est pas limitée à sa surface mais qu’elle peut s’étendre plus loin, il suppose qu’elle est universelle, peut se manifester jusqu’aux astres et provoquer leurs mouvements.

Expression mathématique de la loi de gravitation universelle

Si deux corps A et B possède respectivement une masse mA et mB et que leurs centre de gravité sont séparé par une distance notée “d” alors la valeur de la force de gravitation exercée par A sur B et celle exercée par B sur A peuvent être exprimée par la formule suivante:

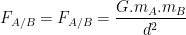
Pour que cette relation soit correcte, il est nécessaire de respecter les unités suivantes:

• Les masses doivent être en kilogramme (kg)
• La distances doit être en mètre (m)
• La forces est exprimée en newton (N)

Par ailleurs la constante de gravitation vaut toujours G = 6,67.10^-11 m³.kg^-1.s^-2

Remarques concernant cette constante

• Etant donnée qu’elle s’exprime dans une unité qui est toujours la même on s’autorise à simplifier la notation en indiquant comme unité “USI”, ce qui signifie unités du système international.
• Sa valeur la plus précise connue est G = 6,67408.10^-11 USI

Astuces pour utiliser la loi de gravitation sans erreur

Les premières applications de cette relation peuvent être laborieuses, voici donc une checklist qui vous évitera les erreurs les plus courantes:

• Vérifier que les masses sont exprimées en kilogramme.
• Vérifier que la distance est exprimée en mètre (et non pas en kilomètre).
• Vérifier que la distance utilisée est bien celle qui sépare les centres de gravité et non pas celle séparant la surface des corps.
• Penser à indiquer le carré de la distance et à en tenir compte dans le calcul.
• Lorsque le calcul est effectué à la calculatrice penser à placer le numérateur et le dénominateur entre parenthèses.
• Penser à présenter le résultat en utilisant la notation scientifique.
• Vérifier l’ordre de grandeur obtenu afin de déceler une éventuelle incohérence révélatrice d’une erreur.

Exemple de calcul de la force de gravitation

Recherche de la valeur de la force de gravitation exercée par par la planète Terre sur un satellite artificiel en orbite autour d’elle.
Données:

• La planète Terre est une sphère de rayon R_T=6740 km de masse M_T=5,97.10²⁴ kg
• Le satellite à une masse m_S = 1,50 tonnes, il est en orbite circulaire autour de la Terre à une altitude h = 20 000 km.

Rappel de l’expression générale de loi de gravitation universelle:

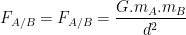
Expression de cette relation à l’aide des données fournies par l’énoncée:

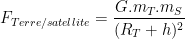
Remarque: la distance séparant le centre de la Terre de celui du satellite est la somme de son altitude et du rayon de la terre (les dimensions du satellites, quelques dizaines de centimètres, peuvent être négligées dans le calcul de cette distance de plusieurs millier de kilomètres)
– Chaque grandeur est remplacée par sa valeur numérique en pensant à la convertir si nécessaire.
La masse du satellite doit être convertie en kilograme m_S = 1,50.10³ kg.
Les distances doivent être converties en mètre: RT = 6740.10³ m et h = 20 000.10³ m
Donc:

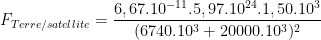
Soit F_{Terre/Satellite} = 852 N

Influence de la masse

La force de gravitation est proportionnelle à chacune des deux masses, par conséquent:

• Une masse deux fois plus élevée (pour l’un des deux corps) correspond à une force de gravitation deux fois plus élevée.
• Une masse trois fois plus élevée (pour l’un des deux corps) correspond à une force de gravitation trois fois plus élevée

etc

Influence de la distance

La force de gravitation a une valeur inversement proportionnelle au carré de la distance qui sépare les centres des deux corps. Par conséquent:

• plus cette distance est élevée et plus la force de gravitation est faible
• si la distance est multipliée par deux alors la valeur de la force de gravitation est divisée par 4 (2 au carré)
• si la distance est multipliée par trois alors la valeur de la force est divisée par 9 (3 au carré)

etc
La force de gravitation diminue très rapidement avec la distance mais ne s’annule jamais totalement, un système subi donc toujours une force gravitationnelle d’un autre système, quel que soit sa distance, même s’il est situé à l’autre bout de l’univers !

Utiliser la loi de gravitation pour calculer une masse

La loi de gravitation fait intervenir la masse des corps qui interagissent il est donc possible d’exprimer cette dernière en fonction des autres grandeurs de la relation:

 

 

 

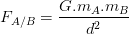
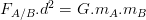
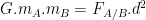
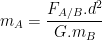
Remarque
L’utilisation de cette relation pour calculer une masse implique que la valeur de la force de gravitation ait pu être déterminée autrement que par la loi de gravitation universelle.

Utiliser la loi de gravitation pour calculer une distance

L’écriture de la loi de gravitation universelle peut aussi être modifiée pour exprimer la distance “d” en fonction des autres grandeurs: