- Définition
- Notation
- Valeur et unité
- Direction et sens
- Point d’application
- Droite d’action
- Déterminer la valeur d’une force
- Vecteur force
Définition
Une force permet de “modéliser” une action mécanique.
En d’autres termes, un phénomène physique (l’action mécanique) est représentée de manière simplifiée (modélisé) par un outil appelé “force” qui résume ses principales caractéristiques: son intensité, sa direction, son sens, la zone où elle s’exerce.
Remarque
Par abus de langage (et pour simplifier) le terme d’ “action” est souvent remplacé par celui force.
Notation
Une force est une grandeur qui se note “F” (comme force !) bien que certaines actions puissent parfois bénéficier d’une notation qui leur est propre (la force gravitationnelle exercée par la Terre, autrement dit le poids est souvent noté avec la lettre “P”) .
Les différentes forces peuvent se distinguer par l’ajout d’indices, on peut peu ainsi trouver des notations du type F1, F2, FA, FB etc. Ces notations on l’avantage d’être courte et simple mais doivent être définies avant utilisation.
La règle générale veut qu’en indice soient indiqués le système auteur de la force puis le système receveur (dans cet ordre) ce qui donne une notation du type Fauteur/receveur
Par exemple:
- La force de gravitation exercée par la Terre sur une pomme se note FTerre/pomme.
- La force magnétique exercée par un aimant sur un clou en fer se note Faimant/clou
- La force de contact exercée par l’eau sur un nageur se note Feau/nageur
- La force exercée par le sol sur un ballon posé sur lui se note Fsol/ballon
Valeur et unité
La valeur d’une force s’exprime en une unité qui est le newton (en hommage à Isaac Newton) de symbole N
Il est envisageable d’utiliser les unités dérivées définies en accolant les préfixes usuels:
- Le kilonewton (kN) avec 1 kN = 103 N
- L’hectonewton (hN) avec 1 hN = 102 N
- Le décanewton (daN) avec 1 daN = 101 N
- Le décinewton (dN) avec 1 dN = 10-1N
- Le centinewton (cN) avec 1 cN = 10-2 N
- Le millinewton (mN) avec 1 mN = 10-3 N
Il est également possible d’utiliser tous les autres préfixes non mentionnés (micro, nano, femto, mega, giga etc). En pratique l’emploi de unités dérivées reste rare (sauf parfois pour le kilonewton ou le millinewton) et la notation scientifique est à privilégier.
Direction et sens
La direction d’une force coïncide avec celle de l’action qu’elle modélise. Pour rappel une direction correspond à un axe qui peut être horizontal, vertical, incliné etc
Le sens de la force coïncide aussi avec celui de l’action modélisée. Pour rappel ce sens peut être vers la gauche, la droite, le haut, le bas, vers un point donné etc.
Point d’application
Il s’agit du point du système receveur où s’exerce l’action mécanique.
- Pour une action localisée le point d’application de la force correspond au point de contact entre l’auteur et le receveur.
- Pour une action répartie en surface on considère qu’il correspond au centre de la surface de contact entre auteur et receveur.
- Pour une action répartie en volume le point d’application correspond au centre du receveur.
Droite d’action
Il s’agit de la droite ayant même direction que la force et passant par le point d’application.
Déterminer la valeur d’une force
La valeur d’une force peut, dans certains cas, être mesurée avec un appareil appelé dynamomètre. Il est constitué d’un ressort qui s’allonge sous l’effet de la force qui lui est appliqué et ses graduations permettent de lire la valeur de la force.
La valeur de certains types de force peut être calculé a l’aide d’une relation, c’est en particulier le cas pour le poids, la force de gravitation, la force électrique, ou la force magnétique.
Dans certaines situations (système immobile ou en mouvement rectiligne uniforme) les forces exercées sur le système se compensent et la valeur d’une force donnée peut être déduite de celles des autre. (voir principe d’inertie) par exemple si un objet de poids 30 N est immobile sur une table alors cette dernière exerce une force de contact qui compense ce poids et vaut aussi 30 N.
Vecteur force
Une force peut associée à un vecteur (le vecteur force). Il est noté de la même manière qu’une force mais la notation est surmontée d’une flèche.
Par exemple, pour la force exercée par la Terre sur une pomme on note le vecteur:
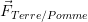
Il possède les caractéristiques suivantes:
- sa direction et son sens son ceux de la force
- son origine coïncide avec le point d’application.
- sa longueur est proportionnelle à la valeur de la force (il faut donc choisir une échelle de représentation adaptée)
La représentation de ces vecteurs sur un schéma est une manière de faire le bilan des forces appliquée à un système
Exemple:

