- Qu’est-ce qu’un électronvolt ?
- Son symbole
- Valeur de l’électronvolt
- Son origine
- Démontrer qu’un électronvolt vaut 1,602177.10-19 J
- Dans quel cas l’utilise-t-on ?
- Convertir les électronvolts en joules
- Convertir les joules en électronvolts
- Les multiples et sous-multiples
- Quelques exemples d’énergies exprimées en électronvolt
- Calculer l’énergie d’un photon en électronvolt à partir de sa longueur d’onde
On le note aussi parfois électron-volt ou électron volt
Qu’est-ce qu’un électronvolt ?
Il s’agit d’une unité d’énergie.
Tout comme le Joule (qui est l’unité d’énergie du système international), l’électronvolt est utilisé dans certaines situations (principalement dans le domaine de la physique des particules) pour exprimer une énergie.
Voir aussi fiche question/réponse “Qu’est-ce qu’un électronvolt ?“
Son symbole
Son symbole est eV
Avec
- «e » comme électron (toujours en minuscule)
- « V » comme Volt (toujours en majuscule)
Valeur d’un électronvolt
Sa valeur est environ de : 1 eV = 1,60.10-19 J
C’est la valeur que l’on utilise le plus souvent et qui figure en général dans les données des exercices.
Si l’on a besoin d’une précision plus élevée on peut utiliser la valeur suivante :
1 eV = 1,602177 x 10-19 J
(Source : Bureau international des poids et mesures: https://www.nist.gov/system/files/documents/pml/div684/fcdc/si_brochure_8.pdf)
Cette valeur ne vous est sans doute pas étrangère puisqu’elle correspond à la valeur que possède (en Coulomb) la charge élémentaire (que l’on retrouve chez le proton et l’électron).
Son origine
L’électronvolt a été défini comme « Le travail reçu par électron, initialement immobile dans le référentiel d’étude, accéléré dans le vide par une différence de potentiel électrique de 1V »
A partir de cette définition on peut retrouver la valeur d’un électronvolt
Démontrer qu’un électronvolt vaut 1,602177.10-19 J
Une différence de potentiel électrique de 1V correspond, par exemple, à champ électrostatique uniforme qui s’exerce une distance de 1m.
On peut schématiser les conditions qui définissent l’électronvolt :
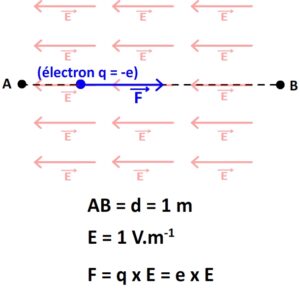
La valeur de la force électrostatique qui s’exerce sur une particule de charge « q » placée dans un champ électrique E est:
|F| = |q| x E
Puisque la particule est un électron de charge -e la force est:
F = |- e| x E
F = e x E
Puisque le champ est uniforme (garde une valeur constante) la force électrostatique est aussi constante pendant ce trajet.
( Voir cours sur les champs électrostatiques: https://webphysique.fr/force-electrique-gravitation-champ/#champ-electrostatique )
Le travail d’une force constante est donné par l’expression :
WAB(
) = .
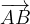
( Voir cours le travail d’une force : https://webphysique.fr/energies-cinetiques-potentielles-et-mecaniques/#Travail-d%E2%80%99une-force )
WAB() = F x AB x cos (α)
WAB()= F x AB x cos (0)
WAB()= F x AB x 1
WAB()= e x E x AB
WAB()= 1,60.10-19 x 1 x 1
WAB() = 1,60.10-19 J
Dans quel cas l’utilise-t-on ?
L’électronvolt est utilisé pour exprimer des énergies de valeur très faible comme par exemple :
- L’énergie d’un photon
- L’énergie des niveaux d’énergie d’un atome
- L’énergie de liaison entre deux atomes
- L’énergie d’ionisation
Pour revoir la méthode qui permet de calculer l’énergie d’un photon voir le cours de première spécialité « modèles ondulatoire et particulaire de la lumière »
La notion d’énergie de liaison est abordée dans le cours de première spécialité « L’énergie de la matière organique »
Convertir les électronvolts en joules
Pour convertir en joule une énergie qui est en électronvolt on multiplie par 1,60.10-19
Exemples
Conversion de 13 eV en joule :
13 x 1,60.10-19 = 2,1.10-18 J
13 électronvolts vaut donc 2,1.10-18 Joules
Conversion de 0,25 eV en joule :
0,25x 1,60.10-19 = 4,0.10–20 J
0,25 électronvolts vaut donc 4,0.10–20 Joules
Conversion de 4,2.10-2 eV en joule :
4,2.10-2 x 1,60.10-19 = 6,7.10–21 J
0,25 électronvolts vaut donc 4,0.10–20 Joules
Convertir les joules en électronvolts
Pour convertir en électronvolts une énergie en Joule on divise par 1,60 x 10-19 .
Remarque : cela revient à multiplier par 1/ 1,60 x 10-19 soit 6,25.1018
Exemples
Conversion de 16.10-19 J en électronvolt :
(16.10-19):(1,60.10-19) = 10 eV
16.10-19 Joules vaut donc 10 électronvolts
Conversion de 8,8.10-19 J en électronvolt :
(8,8.10-19):(1,60.10-19) = 5,5 eV
8,8.10-19 Joules vaut donc 5,5 électronvolts
Conversion de 5,76.10-17 J en électronvolt :
(5,76.10-17):(1,60.10-19) = 360 eV
5,76.10-17 Joules vaut donc 360 électronvolts
Conversion de 3,84.10-20 J en électronvolt :
(3,84.10–20 ):(1,60.10-19) = 0,240 eV
3,84.10–20 Joules vaut donc 0,240 électronvolts
Les multiples et sous-multiples
On peut utiliser les préfixes usuels tels que le kilo, méga, giga, milli, etc pour obtenir les multiples et sous-multiples de l’électronvolt.
Voici les principaux :
- Le milliélectronvolt (meV), 1 meV = 1,60.10-22 J
- Le kiloélectronvolt (keV), 1 keV = 1,60.10-16 J
- Le mégaélectronvolt (MeV), 1 MeV = 1,60.10-13 J
- Le gigaélectronvolt (GeV), 1 MeV = 1,60.10-10 J
- Le Teraélectronvolt (TeV), 1 TeV = 1,60.10-7 J
L’électronvolt est mentionné dans le cours de première spécialité « Modèles ondulatoire et particulaire de la lumière »
Quelques exemples d’énergies exprimées en électronvolt
- Energie cinétique moyenne d’une molécule de gaz à température ambiante (20°C) : 25 meV
- Les photons constituant la lumière visible (de λ = 400 nm à λ= 800 nm) : environ de 1,5 eV à 3 eV
- L’énergie nécessaire pour ioniser l’atome d’hydrogène : 13,6 eV
- L’énergie de masse d’un électron ( relation d’Einstein) : environ 0,5 MeV
- Energie moyenne libérée lorsqu’un noyau d’hydrogène 2 (deutérium) et un noyau d’hydrogène 3 (Tritium) fusionnent pour former un noyau d’hélium 4 : 17,6 MeV
- Energie moyenne libérée par la fission d’un atome d’uranium 235 : 200 MeV
- Energie cinétique d’un moustique en vol : environ 3 TeV
Calculer l’énergie d’un photon en électronvolt à partir de sa longueur d’onde
Pour calculer l’énergie « E » d’un photon à partir de la longueur d’onde (λ) de la lumière il faut faire appel à la relation de Planck-Einstein :
E = h.ν
Cette relation ne fait pas intervenir la longueur d’onde mais la fréquence (ν) par conséquent il faut utiliser l’expression de la fréquence en fonction de la longueur d’onde :
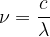
Par conséquent on obtient l’expression suivante :
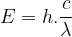
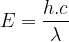
Cette expression permet d’obtenir une énergie exprimée en Joule, pour la convertir en électronvolt il reste à diviser par 1,6.10-19 :
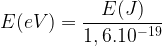
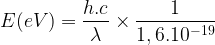
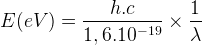
Si l’on calcul la valeur du coefficient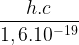 
on obtient :
= 
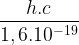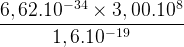
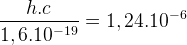
Par conséquent, pour obtenir l’énergie d’un photon directement en électronvolt à partir de la longueur d’onde on peut utiliser la relation :
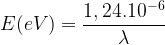
Dans cette relation :
- λ est en mètre (m)
- E(eV) est en électronvolt (eV)
Exemple
Une lumière monochromatique est caractérisée par une longueur d’onde à la limite du domaine visible λ = 400 nm.
Sa fréquence est :
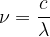
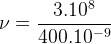
ν = 7,50.1014 Hz
D’après la relation de Planck-Einstein, l’énergie (en joule) d’un photon qui constitue cette lumière est
E = h.ν
E = 6,62.10-34 x 7,50.1014
E = 4,97.10-19 J
Si l’on convertit en électronvolt on obtient
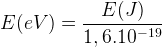
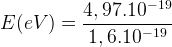
E(eV) = 3,1 eV
Si l’on utilise la relation permettant d’obtenir directement l’énergie en électronvolt :
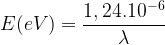
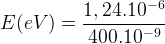
E (eV) = 3,1 eV
On trouve bien la même valeur !
En vidéo “Convertir des électronvolts”:
En vidéo également: “qu’est-ce qu’un électronvolt ?”: