Courant électrique et bilans énergetiques

par

Cours de physique-chimie | première spécialité

Ce cours correspond à la partie “Aspects énergétiques des phénomènes électriques” du programme de première spécialité.

Il est situé dans la partie du programme “L’énergie : conversions et transferts”

REVISER – AUTRES COURS DE PREMIERE SPECIALITE – APPROFONDIR ET DECOUVRIR

Le courant électrique

Notation et unités de l’intensité

L’intensité d’un courant électrique se note I ( I comme Intensité)

Son unité est l’Ampère de symbole A

On utilise parfois aussi le milliampère (mA): 1 A = 1000 mA et 1 mA = 0,001 A

Exemples de conversions:

  • 1,5 A = 1500 mA
  • 0,200 A = 200 mA
  • 630 mA = 0,630 A
  • 1400 mA = 1,400 A

Porteur de charges

Définition:

On appelle “porteur de charge” une particule (élémentaire ou non) possédant une charge électrique non nulle.

Si un milieu comporte des porteurs de charge mobiles alors leur mouvement d’ensemble constitue un courant électrique.

Les principaux porteurs de charges mobiles sont:

Qu’est-ce qu’un courant électrique ?

Un courant électrique correspond à un flux de porteurs de charge mobiles animés d’un mouvement d’ensemble dans la même direction et le même sens.

Courant électrique dans un métal

Les métaux ont une structure particulière, leurs atomes établissent entre eux des liaisons dites “métalliques” qui sont différentes des liaisons covalentes (entre les atomes d’une molécule) ou des liaisons ioniques (entre les ions d’un solide ionique).

Pour simplifier on peut décrire un métal comme un réseau de noyaux atomiques métalliques “baignant” dans un nuage d’électrons qui se déplacent de manière totalement désordonnée.

Ces électrons sont appelés électrons libres, ils circulent d’atome en atome sans qu’il y ait naturellement de mouvement d’ensemble. Les atomes métalliques restent cependant globalement neutres.

Lorsqu’un métal est soumis à une tension électrique alors il s’établit dans ce métal un champ électrique qui influence le mouvement des électrons libres: ils sont soumis à une force électrique qui provoque un mouvement d’ensemble de ces derniers.

Lorsqu’un métal est soumis à une tension il apparait un mouvement d’ensemble des électrons libres qui constitue un courant électrique.

Sens conventionnel du courant électrique

Dans un circuit électrique le sens conventionnel du courant va de la borne positive du générateur à sa borne négative (à l’extérieur du générateur)

Ce sens est souvent indiqué sur un schéma électrique normalisé à l’aide de flèches pleines de couleur rouge (pour les distinguer facilement des autres symboles) situées sur les fils de connexion.

Exemple

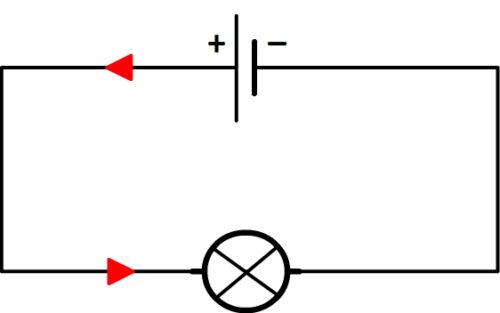
Sens du courant dans un circuit en série simple
Sens du courant dans un circuit en série simple

Remarques

  • Il correspond au sens de circulation d’un porteur de charge positif
  • Lorsqu’on mentionne “le sens du courant” sans autre précision il est sous-entendu qu’il s’agit du sens conventionnel.

Sens de déplacement des porteurs de charge

Dans un circuit électrique:

  • Les électrons (chargés négativement) se déplacent dans le sens inverse au sens conventionnel ( de la borne négative vers la borne positive)

Dans une solution aqueuse:

  • Les anions (ions négatifs) se déplacent, comme les électrons, de la borne négative vers la borne positive.
  • Les cations (ions positifs) se déplacent dans le sens conventionnel du courant, c’est à dire de la borne positive vers la borne négative.

Calculer l’intensité d’un courant

L’intensité est défini comme le flux de charge de charges électriques à travers une section de conducteur électrique.

Si “Q” est la charge totale des porteurs de charge qui traversent la section d’un conducteur électrique pendant une durée Δt alors l’intensité du courant électrique au niveau de cette section correspond au rapport de la charge Q par la durée Δt, ce qui peut se traduire par la formule suivante:

Latex formula

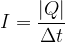
où:

  • I est l’intensité du courant en Ampère (A)
  • |Q| est la valeur absolue de la charge qui traverse la section en Coulomb (C)
  • Δt est la durée qu’il faut à la charge électrique pour passer par la section

Cette relation peut aussi être exploitée pour déterminer la valeur de charge qui traverse la section d’un conducteur:

|Q| = I x Δt

Elle peut aussi être utilisée pour calculer la durée Δt:

Latex formula

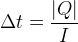
Mesurer l’intensité du courant

Rappel de collège: l’intensité du courant qui circule dans une branche de circuit électrique peut se mesurer à l’aide d’un ampèremètre.

En général on utilise un multimètre en mode ampèremètre (borne COM et A ou mA) avec un calibre sectionné dans la zone adaptée.

L’ampèremètre se branche toujours en série, il est inséré entre deux dipôles du circuit.

Energie et puissance

L’énergie

L’énergie est une grandeur notée “E” (avec parfois des précisions en indice ou entre parenthèse) qui s’exprime en joule (J).

Elle peut exister sous différentes formes (mécanique, lumineuse, sonore, électrique etc) et peut :

  • être convertie (changer de forme, par exemple une énergie électrique peut être convertie en énergie lumineuse et en énergie thermique dans une lampe)
  • être transférée (c’est à dire passer d’un système à un autre)

Quelles que soient les transformations que subit l’énergie elle obéit à une règle de conservation universelle:

La quantité d’énergie totale garde la même valeur.

Autrement dit:

Energie totale d’un système avant conversion = Energie totale du même système après conversions

Energie totale perdue par un système = Energie totale reçue par d’autres systèmes

La puissance

La puissance est une grandeur qui se note “P” et s’exprime en Watt (W)

Elle correspond à l’énergie échangée par un système pendant une durée d’une seconde.

Si un système échange une énergie “E” pendant une durée Δt alors on peut calculer l’énergie grâce à la formule suivante:

E = P x Δt

où

  • E est l’énergie échangée en joule (J)
  • P est la puissance en Watt (W)
  • Δt est la durée pendant laquelle l’énergie est échangée en seconde (s)

On peut en déduire que la puissance est donnée par la relation:

Latex formula

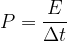
Par ailleurs, la puissance électrique échangée par un dipôle est donnée par la relation:

P = U x I

où:

  • P est la puissance en watt (W)
  • U es la tension en volt (V)
  • I est l’intensité en ampère

Convertisseurs

Définition

Un convertisseur est un système qui convertit l’énergie reçue en une autre forme d’énergie.

Exemples de convertisseurs:

L’efficacité de la conversion est indiquée par son rendement (voir paragraphe sur le rendement)

Les dipôles ohmiques

Qu’est-ce qu’un dipôle ohmique ?

Un dipôle ohmique est aussi parfois appelé:

  • récepteur ohmique
  • résistor
  • résistance

C’est un récepteur qui se caractérise uniquement par sa résistance, la tension à ses bornes obéit à la loi d’Ohm et il convertit la totalité de l’énergie électrique qu’il reçoit en énergie thermique (effet Joule)

Loi d’ohm

Qu’est-ce que la loi d’ohm ?

Il s’agit de la loi qui permet d’exprimer la tension aux bornes d’un dipôle ohmique en fonction de sa résistance et de l’intensité du courant électrique reçu.

Qu’indique la loi d’Ohm ?

D’après la loi d’Ohm, la tension aux bornes d’un conducteur ohmique est proportionnelle à l’intensité du courant qui circule dans ce conducteur et le coefficient de proportionnalité correspond à la valeur de sa résistance “R”

Expression de la loi d’Ohm par une formule

U = R x I

Avec:

  • U la tension aux bornes du conducteur ohmique en volt (V)
  • R, la résistance du dipôle ohmique en Ohm (Ω) (lettre grecque oméga)
  • I l’intensité du courant en Ampère (A)
Que peut-on calculer grâce à la loi d’ohm ?
  • On peut déterminer la tension aux bornes du dipôle ohmique si l’on connaît sa résistance et l’intensité du courant grâce à la formule U = R x I
  • On peut déterminer l’intensité du courant qui circule dans un dipôle ohmique grâce à la relation Latex formula
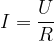
  • On peut déterminer la valeur d’une résistance grâce à la relation Latex formula

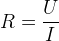
Effet Joule

Qu’est-ce que l’effet Joule ?

L’effet Joule désigne la conversion d’énergie électrique en énergie thermique par un dipôle ohmique parcouru par un courant électrique.

Un dipôle ohmique convertit la totalité de l’énergie électrique qu’il reçoit en énergie thermique.

Comment exploiter l’effet Joule ?

L’effet Joule peut être exploité pour produire de la chaleur, tout les dispositifs électriques chauffant reposent sur lui et comportent des dipôles ohmiques (des résistances électriques) qui convertissent l’énergie électrique en énergie thermique.

L’effet Joule est par exemple exploité pour produire de la chaleur dans:

  • Les radiateurs électriques
  • Les plaques de cuisson électriques
  • Les fours électriques
  • Les fers à repasser
  • Les sèche-cheveux

L’effet Joule provoque une perte d’énergie

Tous les conducteurs électriques, et par conséquent tous les dipôles et systèmes électriques, possèdent une certaine résistance électrique (seuls les matériaux supraconducteurs ont une résistance électrique nulle).

Par conséquent ils sont le siège d’un effet Joule qui convertit une partie de l’énergie électrique reçue en énergie thermique. Cette énergie thermique provoque une élévation de leur température, elle est en partie transférée au milieu extérieur.

La conséquence de l’effet Joule est donc:

  • de provoquer un échauffement du convertisseur susceptible de l’endommager
  • de provoquer un échauffement du milieu extérieur parfois dangereux (incendie d’origine électrique)
  • de conduire à une dissipation d’énergie qui diminue le rendement

Calculer la puissance dissipée par effet Joule

La puissance dissipée par effet est donnée par la relation suivante:

P = U I

P = (R.I) .I

P = R.I2

Générateur réel de tension continue

Comme tout dipôle, un générateur possède une résistance interne “r” qui influence la valeur de la tension qu’il délivre.

On peut modéliser un générateur réel comme l’association en série d’un générateur idéal de tension “E” constante et d’un dipôle ohmique de résistance “r”

Par conséquent la tension UAB aux borne d’une générateur réelle est:

UAB = E – r.I

La caractéristique d’un générateur est a donc le profil suivant:

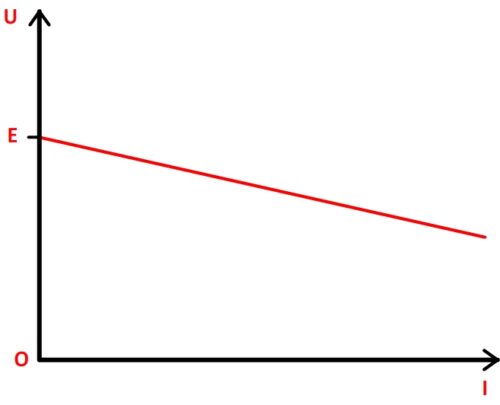
Caractéristique d'un générateur réel
Caractéristique d’un générateur réel

Il s’agit d’une fonction affine décroissante:

  • dont l’ordonnée à l’origine est “E”
  • dont le coefficient directeur est “r”

La présence de cette résistance a pour conséquences:

  • La tension fournie n’est pas rigoureusement constante, elle diminue lorsque l’intensité du courant augmente.
  • Une partie de l’énergie est dissipée par effet Joule.

Rendement

Par définition un convertisseur convertit l’énergie qu’il reçoit en une autre forme d’énergie qui nous est utile cependant tout processus de conversion d’énergie entraîne inévitablement des “pertes”.

Chaine d'energie d'un convertisseur

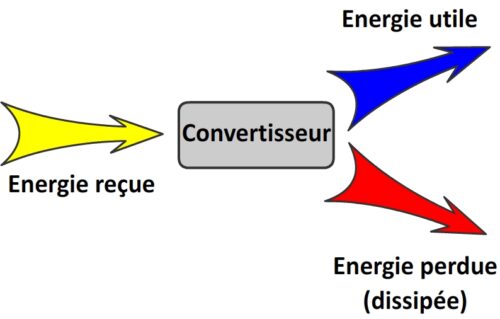
Une proportion variable de l’énergie “investie” est perdue sous forme thermique (en raison de l’effet Joule, à cause de frottements etc).

Le rendement est une grandeur qui traduit l’efficacité d’un convertisseur

Le rendement se note le plu souvent : η (lettre grecque êta) et il correspond au rapport de l’énergie utile par l’énergie reçue.

Il peut se calculer grâce à la formule suivante:

Latex formula

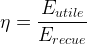
où les deux énergies sont exprimées dans la même unité (par exemple en joule)

étant donné que l’énergie est proportionnelle à la puissance et et au temps de l’échange, le rendement peut aussi se calculer grâce à la formule suivante:

Latex formula

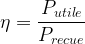
où les deux puissances sont exprimées dans la même unité (par exemple en watt)

Remarque

Le rendement peut aussi par fois s’exprimer sous la forme d’un pourcentage, pour cela il suffit de rajouter un facteur “100” aux formules précédentes, ce qui donne:

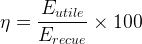Latex formula ou Latex formula

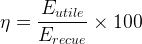
Le rendement est une grandeur comprise entre 0 et 1:

  • si le redement est nul (0) alors le convertisseur n’a pas permis d’obtenir la forme d’énergie souhaitée
  • Si le rendement est de “1” alors il est maximal, il s’agit d’un convertisseur idéal (qui n’existe pas en pratique) permettant de convertir l’intégralité de l’énergie reçue en énergie utile sans pertes.
  • Plus le rendement est proche de “1” et plus la conversion est efficace.

Bilan d’énergie et de puissance dans un circuit électrique

Le principe de conservation de l’énergie implique que l’énergie cédée par un système est nécessairement reçue par un ou plusieurs autres systèmes.

Si l’on applique ce principe à circuit électrique alors:

L’énergie fournie par le générateur correspond à la somme des énergies reçues par les récepteurs du circuit.

Egénérateur = Erécepteur1 + Erécepteur2 + Erécepteur3 …..

La conservation de l’énergie implique aussi la conservation des puissances:

La puissance du générateur correspond à la somme des puissances reçues par les récepteurs du circuit:

Pgénérateur = Précepteur1 + Précepteur2 + Précepteur3 …..

A réviser

Cours de seconde:

Les autres cours de première spécialité

Pour approfondir et découvrir