Ondes et signaux – Signaux et capteurs
- Qu’est-ce qu’un circuit électrique ?
- Maille d’un circuit
- Noeud
- Branche
- Circuit en série
- Circuit en dérivation
- Générateur
- La tension électrique
- L’intensité
- Flèche et signe d’une tension
- Loi des mailles
- Loi des noeuds
- Loi d’Ohm
- Caractéristique d’un dipôle
- Point de fonctionnement d’un récepteur
Qu’est-ce qu’un circuit électrique ?
Un circuit électrique est une association de dipôles (au moins un générateur et un récepteur) connectés entre eux où le courant électrique peut circuler.
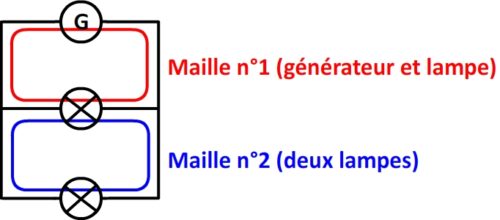
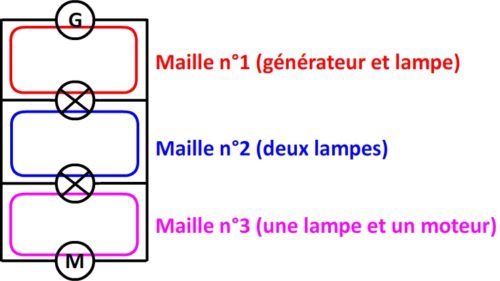
Maille d’un circuit
Une maille est un ensemble de dipôles connectés entre eux de manière à former une boucle.
Noeud
Un noeud est un point du circuit électrique où sont connectés au moins trois dipôles différents.
Seuls les circuits en dérivation comportent des noeuds.
Exemple
Branche
Une branche est une portion de circuit située entre deux noeuds qui se suivent.
Dans une branche, tous les dipôles sont branchés les uns à la suite des autres (en série)
Circuit en série
Un circuit est en série s’il comporte une seule maille et ne forme donc qu’une seule boucle. Les dipôles y sont tous connectés les uns à la suite des autres.
Exemples
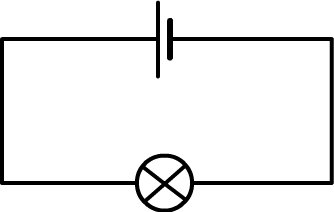
Un circuit comportant seulement deux dipôles est toujours un circuit en série !
Circuit en dérivation
Un circuit est en dérivation s’il comporte un minimum de deux mailles. Dans un circuit en dérivation il y a donc toujours au moins deux boucles et deux noeuds.
Exemples
Générateur
Un générateur est un dipôle produisant (générant) une tension électrique à ses bornes (positive et négative) même lorsqu’il est isolé (non connecté).
Dans un circuit électrique fermé cette tension donne naissance à un courant électrique.
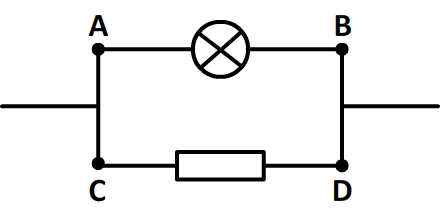
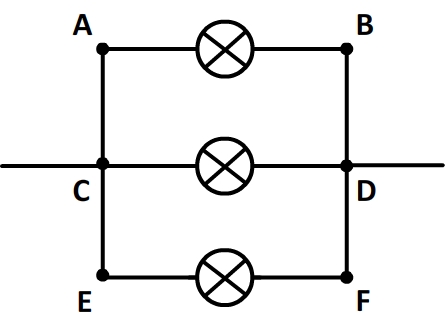
La tension électrique
La tension est une grandeur physique qui s’exprime toujours entre deux points d’un circuit électrique (en général les bornes d’un dipôles).
Elle se note “U” et son unité est le volt (de symbole “V“)
Unicité de la tension: les tensions aux bornes de deux dipôles branchés en dérivation sont les mêmes.
Exemples
L’intensité
C’est une grandeur qui exprime le débit du courant électrique en un point donné d’un circuit.
Elle se note “I” et son unité est l’Ampère (de symbole “A“).
Le courant circule toujours de la borne positive (+) du générateur du circuit vers la borne négative (-).
Unicité de l’intensité en série: lorsque des dipôles sont branchés en série le courant qui circule dans ces dipôles garde la même intensité.
Conséquences de la loi d’unicité de l’intensité:
– L’intensité du courant garde la même valeur en tous points d’une branche.
– L’intensité du courant a même valeur en tous points d’un circuit en série.
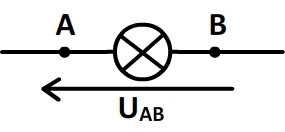
Flèche et signe d’une tension
La tension aux bornes d’un dipôle peut être comptée positivement ou négativement et pour déterminer facilement le signe d’une tension on lui associe une flèche:
Une tension UAB (entre un premier point A et un deuxième point B) est associée à une flèche qui pointe vers le point A (le premier point)
Exemples
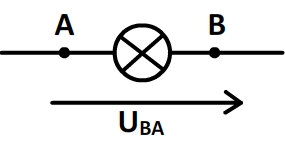
Pour pouvoir associer un signe à une tension il est nécessaire de choisir un sens de parcours de la maille qui est en général précisé à l’aide d’une flèche tournante.
Attention:
- le sens de parcours d’une maille n’est pas nécessairement le même que le sens de circulation du courant électrique.
- Le signe que l’on donne aux tensions n’est exploité que pour utiliser la loi des mailles.
Si la flèche d’une tension est dans le même sens que l’orientation d’une maille alors cette tension est décomptée positivement.
Si la flèche d’une tension est opposée au sens d’orientation d’une maille alors cette tension est décomptée négativement.
Exemples
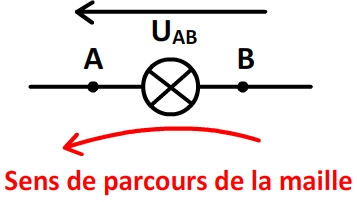
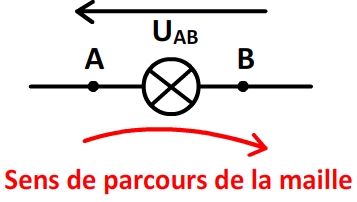
Des tension exprimées dans des ordre inverses ont des signes opposés:
UAB = – UBA
La loi des mailles
C’est une loi concernant les tensions, elle permet d’exprimer une relation entre la tension des dipôles d’une même maille.
Enoncé de la loi des mailles:
Dans une même maille la somme de toutes les tensions est nulle
Pour appliquer une la loi des mailles il est donc nécessaire:
- de préciser la maille considérée
- de choisir un sens de parcours de la maille
- de tenir compte de la tension de chaque dipôle et de son signe
Exemple
Soit le circuit suivant:
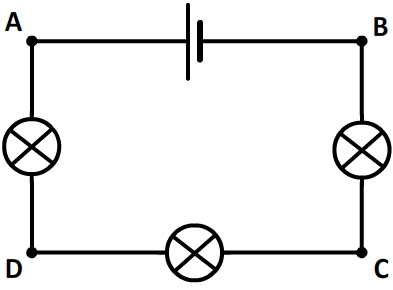
D’après la loi des mailles la somme des tensions est nulle d’où la relation:
UAB + UBC + UCD + UDA = 0
Pour exploiter des tensions dont le signe est donné dans le sens inverse on peut être amené à modifier cette relation en remplaçant certaine tension par leur opposée.
On peut par exemple aussi écrire:
-UBA + UBC + UCD + UDA = 0
ou
UAB – UCB – UDC – UAD = 0
La loi des noeuds
C’est une loi concernant l’intensité du courant électrique: elle permet d’exprimer une relation entre les intensités des courants circulant dans les dipôles connectés à un même noeud.
Enoncé de la loi des noeuds:
L’intensité totale des courants entrant dans un noeud est égale à l’intensité totale des courants sortant de ce noeud.
Pour appliquer la loi des noeuds il faut:
- repérer un noeud.
- recenser les courants entrants (flêche orientée vers le noeud).
- recenser les courants sortants (flêche s’éloignant du noeud).
- Exprimer la somme des intensités des courants entrants.
- Exprimer la somme des intensités des courants sortants.
- Exprimer l’égalité des deux sommes précédentes puis isoler l’intensité inconnue.
Exemples

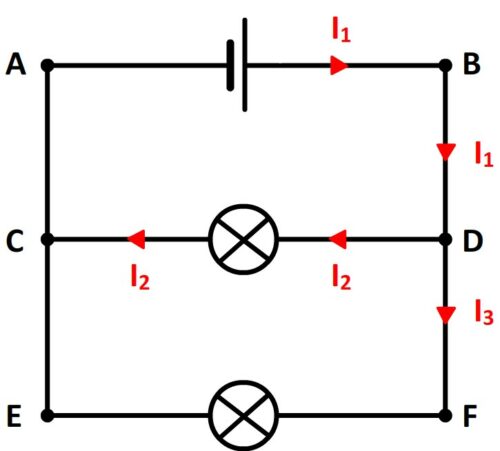
Loi des noeuds appliquée au noeud D:
- L’intensité totale des courants entrants est I1
- L’intensité totale des courants sortants est I2 + I3
- D’après la loi des noeuds: I1 = I2 + I3
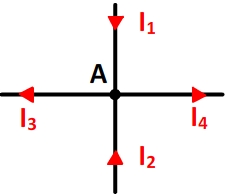
I1 + I2 = I3 + I4
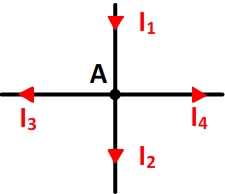
I1 = I2 + I3 + I4
La loi d’Ohm
La loi d’Ohm exprime la relation entre la tension “U” et l’intensité “I” pour un dipôle ohmique de résistance “R”.
Elle peut être exprimée par la formule suivante:
U = R x I
où:
- U est en volt (V)
- R est en ohm (Ω)
- I est en ampère (A)
Caractéristique d’un dipôle
La caractéristique d’un dipôle est un graphique présentant l’évolution de la tension à ses bornes en fonction de l’intensité du courant électrique.
Il s’agit donc de la représentation de la fonction U = f(I) avec:
- L’intensité “I” en abscisses
- La tension “U” en ordonnées
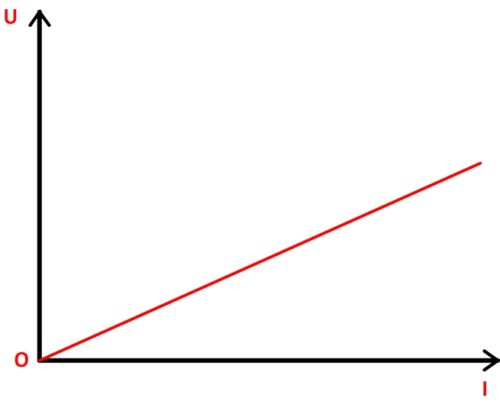
Par exemple la caractéristique d’un dipôle ohmique est une fonction linéaire (droite passant par l’origine) dont le coefficient directeur a même valeur que la résistance.
Exemples
Remarque
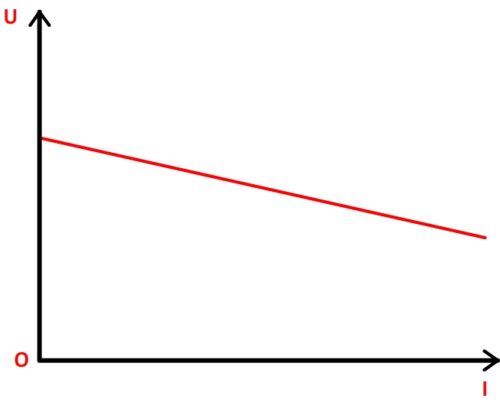
Un générateur possède une résistance interne qui conduit à une diminution de la tension fournie lorsque le courant débité augmente.
Point de fonctionnement d’un récepteur
Le point de fonctionnement d’un récepteur correspond aux couples de valeur tension/intensité caractérisant le fonctionnement de ce récepteur avec un générateur donné.
Le point de fonctionnement P(I,U) d’un récepteur avec un générateur correspond à la tension et l’intensité du courant de ce récepteur lorsque ce dernier est directement connecté aux bornes du générateur.
Pour obtenir le point de fonctionnement d’un récepteur il faut:
- Tracer la caractéristique du récepteur.
- Tracer la caractéristique du générateur sur le même graphe
- Déterminer le point d’intersection entre les deux caractéristiques
- Déterminer les coordonnées du point précédent qui correspondent au point de fonctionnement.
Exemple
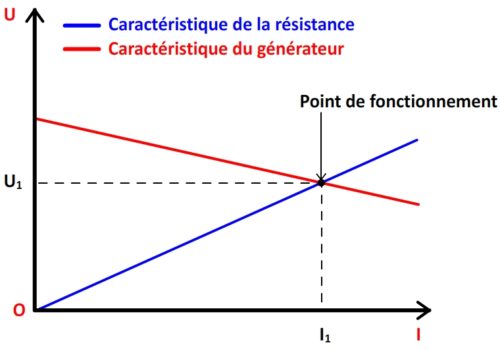
Le point de fonctionnement a pour coordonnées (I1 ; U1)
Les autres cours de physique-chimie niveau seconde
- Corps purs et mélanges au quotidien
- Les solutions aqueuses, un exemple de mélange
- Du macroscopique au microscopique, de l’espèce chimique à l’entité
- Le noyau de l’atome, siège de sa masse et de son identité
- Le cortège électronique de l’atome définit ses propriétés chimiques
- Vers des entités plus stables chimiquement
- Transformation physique
- Transformation chimique
- Transformation nucléaire
- Décrire un mouvement
- Modéliser une action sur un système
- Principe d’inertie
- Emission et perception d’un son
- Vision et image
- Circuits électriques
- Capteurs
