Partie du programme d’enseignement scientifique de première concerné: Son et musique, porteurs d’informations: Musique, l’art d’entendre les nombres
Exercice faisant partie du sujet n°1 ( G1CENSC02392 G1CENSC02392)

Partie A. Gamme tempérée

Correction de la question 1
Par définition l’intervalle entre deux notes constitue une octave si le rapport entre leurs fréquences est de 2.
Si la note “1” de fréquence f1 et la note “2” de fréquence f2 sont séparées d’une octave alors:
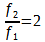
Correction de la question 2
Si une octave commence par une note “0” de fréquence f0 alors la note constituant la limite de cet octave (qui est aussi la première note de l’octave suivante) à une fréquence deux fois plus élevée à soir 2xf0
Cette octave est constituée de 12 notes, la première de fréquence f0, la deuxième de fréquence f1 la douxième de fréquence f11.
Chaque note ns’obtient à partir de la précédente en multipliant par un rapport “r”:
f1 = f0 x r
f2 = f1 x r = f0 x r x r = f0 x r2
f3 = f2 x r = f0 x r2 = f0 x r3
et ainsi de suite…
Pour la note n° “n” on aura donc fn = f0 x rn
La dernière note de l’octave aura pour fréquence f0xr11
La fréquence de la note qui débute l’octave suivante aura donc comme fréquence f0 x r12
La fréquence de la note qui débute l’octave suivante peut s’exprimer soit par “ f0 x r12” soit par “2xf0”
Par conséquent on peut écrire l’égalité suivante:
f0 x r12= 2xf0
Si l’on simpifie par f0 dans les deux membres:
r12= 2
( r12)1/12 =(2)1/12
r12 x 1/12 =(2)1/12
r1 =(2)1/12
r =(2)1/12
Le rapport “r” entre les fréquences de deux notes successives correspond donc bien à la racine douzième de 2

Correction de la question 3
Chaque note appartenant à une octave de la gamme tempérée peut être obtenue à partir de la précédente en multipliant la fréquence de la précédente par le rapport “r”
On peut donc obtenir la note manquante (le Sol3#) à partir la précédente (Sol3):
f(Sol3#) = f(Sol3) x r
f(Sol3#) = 392,0 x 21/12
f(Sol3#) = 415,3 Hz
La fréquence de la note manquante est donc de 415,3 Hz
Partie B. Application aux frettes de la guitare classique
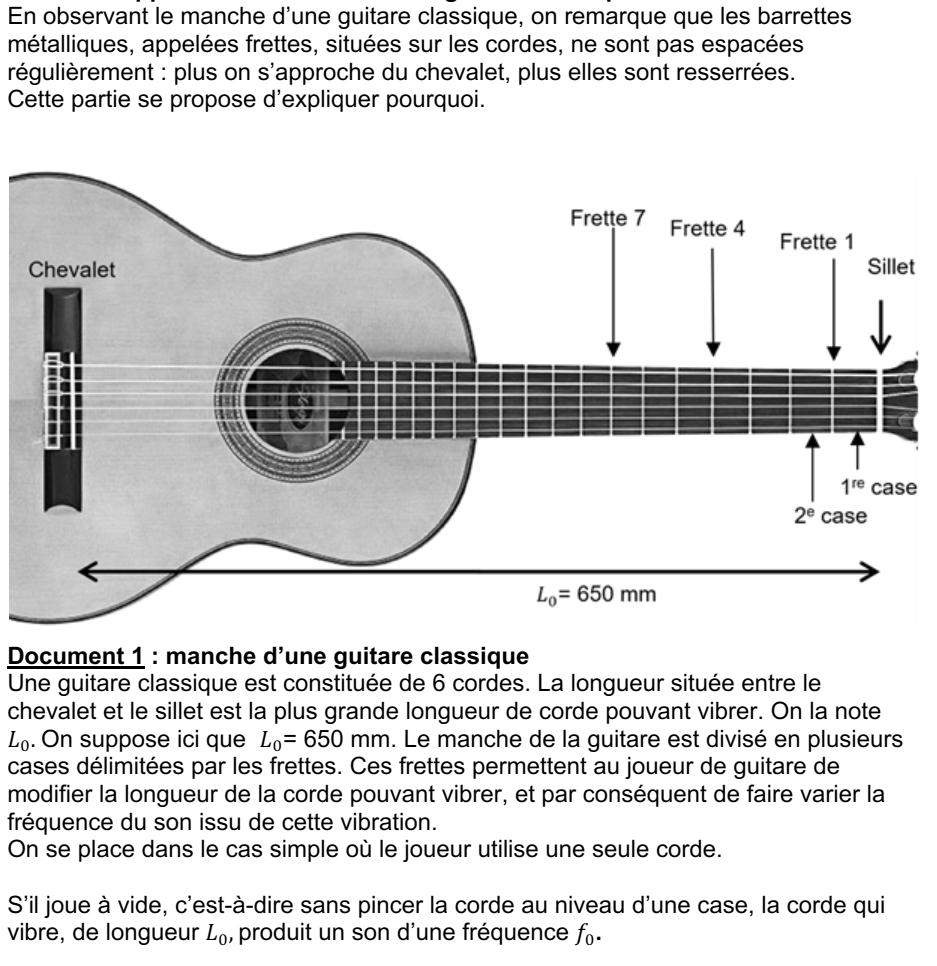

Correction de la question 4-a
Le Mi4 possède une fréquence deux fois plus élevée que le Mi3 or un son est d’autant plus aigu que sa fréquence est élevée par conséquent:
Le Mi4, dont la fréquence est plus élevée que le Mi3, est donc plus aigu que ce dernier.

Correction de la question 4-b
Il existe la relation suivante entre la fréquence à vide (f0), la longueur de la corde vibrant à vide (L0) et la fréquence fn de la note obtenue en pinçant la frette “n” lorsque la longueur de la corde vibrante est Ln:
Ln x fn = L0 x f0
Lorsque la frette n°12 est pincée la longueur de corde vibrante est L12 et la fréquence de la note obtenue est (d’après l’énoncé) f12 = 2 x f0 donc en remplaçant dans la relation précédente on obtient:
L12 x (2f0 ) = L0 x f0
Si l’on simplifie par f0 dans les deux membres de l’égalité on obtient:
L12 x 2 = L0
Donc:
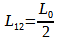

Correction de la question 5
D’après l’énoncé:
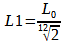
Cette longueur (L1) correspond à la longueur totale de la corde (L0) diminuée de la longueur de la première case L(case1) donc:
L(case1) = L0 – L1
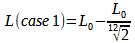
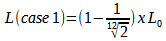
Ce qui donne environ:
L(case1) = 0,0561 x L0
