Cours de physique-chimie | première spécialité
Ce cours correspond à la partie “Interactions fondamentales et introduction à la notion de champ” du programme de première spécialité.
Il est situé dans la partie du programme “Mouvement d’un système”
- Vecteur variation de vitesse d’un système
- Vecteur force totale
- Relation entre le vecteur variation de vitesse et la force totale
- Déterminer le vecteur variation de vitesse à partir de la force totale
- Déterminer la force totale
- Mouvement d’un système soumis à une force totale constante
- Caractéristiques d’une force totale constante
- Exemples de force totale constante
- Variation de la vitesse
- Système immobile au début de son mouvement
- Cas d’une vitesse initiale ayant même sens et direction que la force totale
- Cas d’une vitesse initiale et d’une force totale de même direction et de sens opposés.
REVISER – AUTRES COURS DE PREMIERE SPECIALITE – APPROFONDIR ET DECOUVRIR
Vecteur variation de vitesse d’un système
Définition
Lorsqu’un système en mouvement dans un référentiel donné passe d’un point n°1 caractérisé par un vecteur vitesse 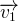 à un point n°2 caractérisé par un vecteur vitesse
à un point n°2 caractérisé par un vecteur vitesse 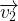 alors le vecteur variation de vitesse correspond à la différence vectorielle des deux vecteurs vitesse.
alors le vecteur variation de vitesse correspond à la différence vectorielle des deux vecteurs vitesse.
Notation et unité
Ce vecteur variation de vitesse se note en général 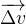 (Δ est lettre grecque delta majuscule associée aux variations de grandeur)
(Δ est lettre grecque delta majuscule associée aux variations de grandeur)
Sa norme (sa valeur) 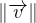 s’exprime dans la même unité qu’une vitesse: en mètre par seconde (m.s-1)
s’exprime dans la même unité qu’une vitesse: en mètre par seconde (m.s-1)
Expression du vecteur variation de vitesse
D’après sa définition on peut exprimer le vecteur variation de vitesse par la relation:
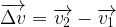
Les vecteurs vitesse peuvent être déterminés graphiquement ( voir cours de seconde sur la description d’un mouvement: https://webphysique.fr/decrire-mouvement/ )
Détermination graphique du vecteur variation de vitesse
Le vecteur variation de vitesse peut aussi être déterminé graphiquement par soustraction du vecteur vitesse n°2 au vecteur vitesse n°1.
Cette soustraction revient à ajouter le vecteur n°2 à l’opposée du vecteur n°1, c’est à dire un vecteur de même direction et longueur que le vecteur n°1 mais de sens opposé
Cette soustraction se fait en général par construction graphique. (voir exemple ci-dessous)
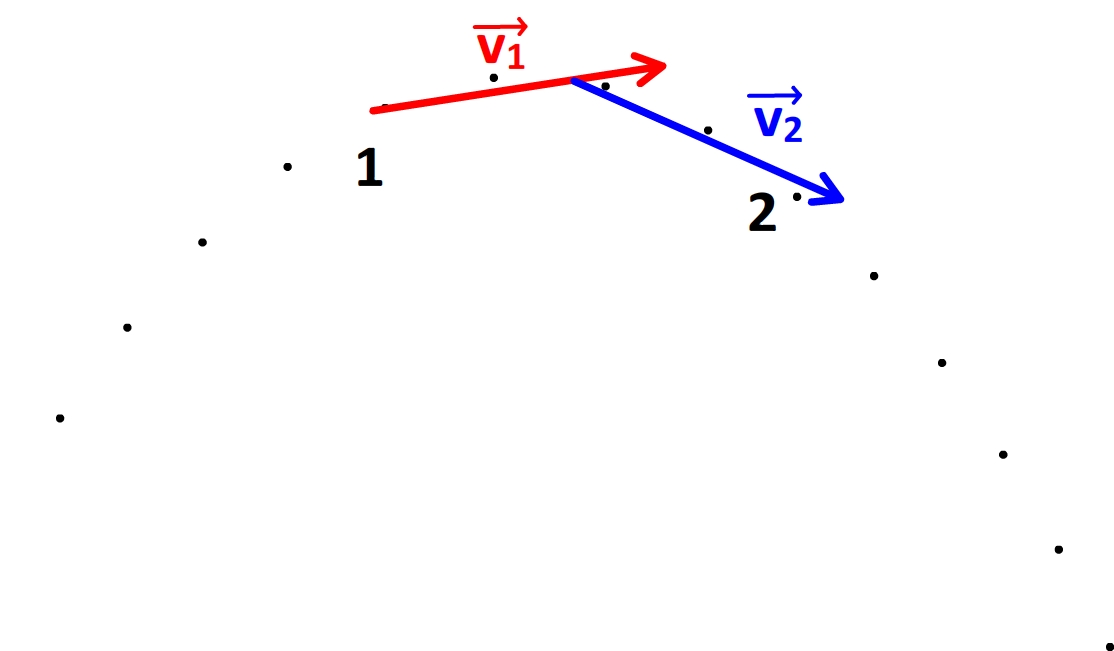
- Etape n°2: reporter le vecteur vitesse
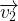 et construire le vecteur vitesse
et construire le vecteur vitesse 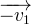 qui correspond à l’opposé du vecteur vitesse
qui correspond à l’opposé du vecteur vitesse 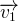 (même direction, même longueur mais sens opposé)
(même direction, même longueur mais sens opposé)
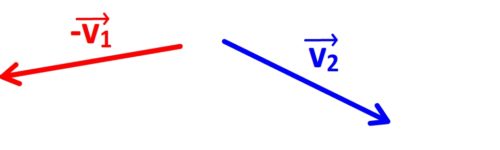
- Etape n°3: réaliser graphiquement la somme
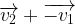 en traçant le vecteur
en traçant le vecteur 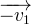 à la suite du vecteur
à la suite du vecteur 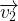 (l’origine du vecteur
(l’origine du vecteur 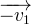 correspond à la pointe de la flèche du vecteur
correspond à la pointe de la flèche du vecteur 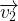 ).
).
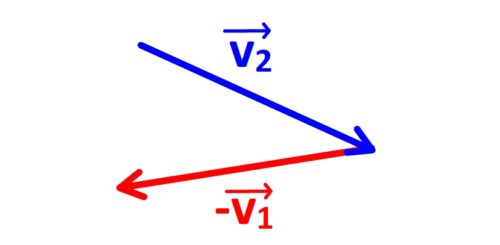
Etape 4: le vecteur variation de vitesse 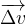 est obtenu en joignant l’origine du vecteur
est obtenu en joignant l’origine du vecteur 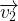 à la pointe du vecteur
à la pointe du vecteur 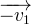 .
.
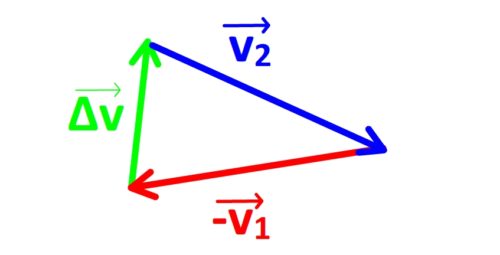
Cas particulier d’un mouvement rectiligne
Dans le cas particulier d’un mouvement rectiligne, c’est à dire d’un mouvement dont la trajectoire est une droite, alors:
- Les vecteur vitesses ont tous même direction que la trajectoire.
- Les vecteurs variation de vitesse ont également même direction que la trajectoire.
- Si la vitesse est croissante alors le vecteur variation de vitesse est orienté dans le même sens que les vecteurs vitesses (et que le mouvement)
- Si la vitesse est décroissante alors le vecteur variation de vitesse est orienté dans le sens opposé des vecteurs vitesse (et du mouvement).
- La norme du vecteur vitesse correspond simplement à la valeur absolue de la différence des normes du vecteur vitesse
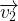 et du vecteur vitesse
et du vecteur vitesse 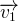 :
: 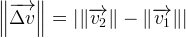
Vecteur force totale
Le vecteur force totale peut aussi parfois être appelé “résultante des forces”.
Notation et unité
Il se se note en général 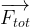 (tot pour “totale”) et l’unité de sa norme est celle d’une force: le Newton (N).
(tot pour “totale”) et l’unité de sa norme est celle d’une force: le Newton (N).
Définition
Il correspond à la somme des vecteurs forces qui s’appliquent au système étudié.
Expression du vecteur force totale
Si le système étudié n’est soumis à aucune force alors 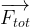 =
= 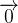
Si le système n’est soumis qu’à une seule force 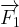 (le poids par exemple) alors
(le poids par exemple) alors 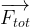 =
= 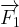
Si le système est soumis à deux forces (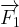 et
et 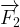 ) alors
) alors 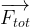 =
= 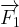 +
+ 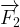
Si le système est soumis à trois forces ( 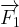 ,
, 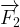 et
et 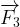 ) alors
) alors 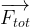 =
= 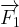 +
+ 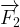 +
+ 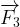 etc ….
etc ….
On peut aussi noter d’une manière plus générale que 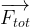 =
= 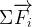
Détermination du vecteur force totale
Il peut être obtenu graphiquement en additionnant les les différents vecteurs forces, c’est à dire en les représentant les uns à la suite des autres.
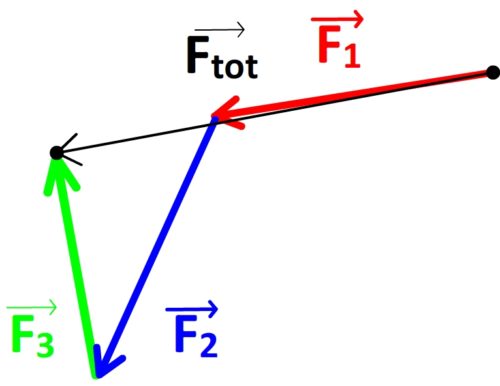
Exemples de détermination graphique du vecteur force totale pour un système soumis à trois forces (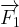 ,
, 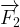 et
et 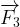 ).
).
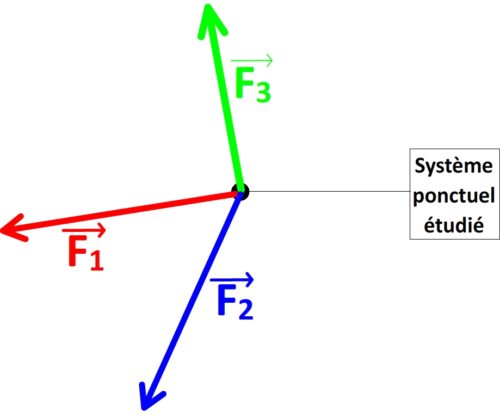
- Etape n°2: Additionner les trois vecteurs forces,
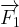 est représenté en premier,
est représenté en premier, 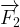 est représenté à la suite de
est représenté à la suite de 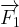 (en faisant coïncider son origine avec la pointe de
(en faisant coïncider son origine avec la pointe de 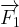 ).
). 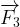 est représenté à la suite de
est représenté à la suite de 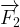 , ( en faisant coïncider l’origine de
, ( en faisant coïncider l’origine de 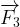 avec la pointe de
avec la pointe de 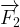 )
)
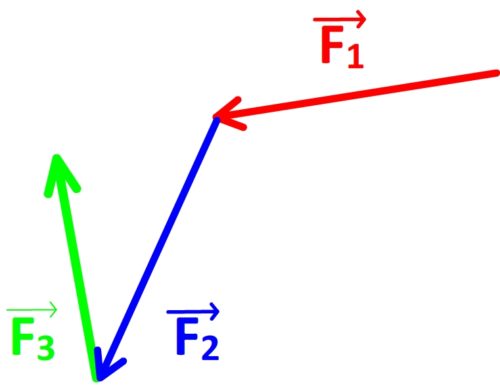
- Etape n°3: l’origine du vecteur
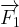 est joint à l’extrémité du vecteur
est joint à l’extrémité du vecteur 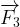 pour obtenir le vecteur force totale
pour obtenir le vecteur force totale 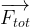
Relation entre le vecteur variation de vitesse et la force totale
Conditions d’utilisation
Cette relation est vérifiée pour deux points voisins (dans l’espace et dans le temps) de la trajectoire du système étudié.
Elle peut aussi être vérifiée pour deux points quelconques d’une trajectoire (aussi éloignés qu’on le souhaite) dans le cas particulier d’un système soumis à des forces constantes (en valeur, en direction et en sens)
Formule
On considère deux points très voisins de la trajectoire d’un système de masse “m” étudié dans un référentiel où:
- Le point n°1 est atteint à la date t1 , le vecteur vitesse est
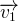
- Le point n°2 est atteint à la date t2, le vecteur vitesse est
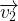
- Entre ces deux points le système est soumis à une force totale
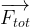
Il existe alors la relation qui se traduit par la relation suivante:
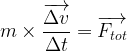
Il s’agit d’une relation vectorielle (entre le vecteur variation de vitesse et le vecteur force totale) où :
- m est la masse du système (en kg)
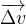 est le vecteur variation de vitesse avec
est le vecteur variation de vitesse avec 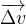 =
= 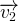 –
– 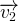 où la norme du vecteur
où la norme du vecteur 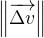 s’exprime en mètre par seconde (m.s-1)
s’exprime en mètre par seconde (m.s-1)- Δt est la durée du mouvement du point 1 au point 2 avec Δt = t2 – t1 qui s’exprime en seconde (s)
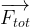 est le vecteur force totale dont la norme s’exprime en Newton (N)
est le vecteur force totale dont la norme s’exprime en Newton (N)
Cette relation peut aussi s’exprimer sous forme algébrique:
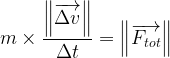
Cas particulier d’un système soumis à des forces constantes
Si lors d’un mouvement la force totale est constante, c’est à dire qu’elle garde la même direction, le même sens et la même valeur, alors la relation précédente ne s’applique plus seulement à deux points voisins de la trajectoire mais à deux points quelconques de la trajectoire.
Si 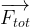 est constante alors la relation est valable entre n’importe quelle paire de points de la trajectoire.
est constante alors la relation est valable entre n’importe quelle paire de points de la trajectoire.
Dans quel but utiliser cette relation ?
- Elle permet d’étudier l’évolution du vecteur vitesse lorsque les caractéristiques (valeur, direction, sens) de la force totale sont connues. Elle permet, en particulier, de déterminer si le mouvement est accéléré (vitesse croissante) ou ralenti (vitesse décroissante).
- Elle permet aussi de déterminer la force totale exercée sur un système en mouvement lorsque l’évolution de sa vitesse est connue.
Déterminer le vecteur variation de vitesse à partir de la force totale
Formule utilisée pour calculer le vecteur variation de vitesse
D’après la relation suivante:
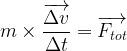
On peut isoler le vecteur variation de vitesse et obtenir son expression:
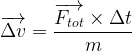
Utiliser la formule pour trouver le vecteur variation de vitesse
Pour déterminer le vecteur variation de vitesse il faut donc:
- connaître la durée (Δt) du mouvement étudié (en seconde).
- connaître la masse du système étudié (en seconde).
- déterminer la force totale qui s’exerce sur le système pendant son mouvement.
La formule (du paragraphe précédent) est utilisée pour trouver d’une part la direction du vecteur variation de vitesse et d’autre part la norme de ce vecteur.
Il résulte de cette relation que le vecteur variation de vitesse 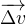 :
:
- a même direction que le vecteur force totale
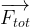
- a pour valeur
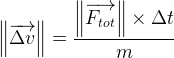
Interprétation
Que peut-on déduire de l’expression du vecteur variation de vitesse ?
Cette relation indique que:
- La variation du vecteur vitesse se fait dans le même sens que la force totale, par conséquent si la force totale a une direction et un sens identiques à ceux du vecteur vitesse alors la vitesse augmente (et inversement si leur sens sont opposés alors la vitesse diminue)
- La variation de vitesse est d’autant plus importante que la masse du système est faible.
- La variation de vitesse est proportionnelle à la durée, si celle-ci augmente alors la variation de vitesse augmente aussi.
Cas où la somme des forces est nulle
Si la force totale est nulle alors l’expression du vecteur variation de vitesse devient:
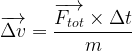
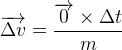
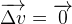
Par conséquent le vecteur vitesse:
- garde la même direction
- garde la même valeur
Dans ces conditions le mouvement est rectiligne uniforme.
On peut interpréter ce résultat en indiquant que si un système est soumis à une force totale nulle (autrement dit à des forces qui se compensent) alors le mouvement du système est rectiligne uniforme: on retrouve ainsi le principe d’inertie déjà vu en seconde.
Le principe d’inertie est une conséquence de la relation entre la variation de vitesse et la force totale
Cas où la somme des forces est constante
Voir pargaphe consacré à l’étude du mouvement d’un système soumis à une force totale constante.
Déterminer la force totale
D’après la relation suivante:
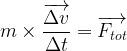
ou encore
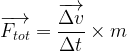
D’après cette relation, le vecteur force totale:
- a même direction et même sens que le vecteur variation de vitesse
- a une norme qui peut être calculée grâce à la relation:
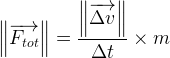
Mouvement d’un système soumis à une force totale constante
Caractéristiques d’une force totale constante
La force totale est constante si le vecteur force totale garde au cours du mouvement:
- la même direction
- le même sens
- la même norme
Exemples de forces totales constantes
Exemple de situations de mouvement d’un système soumis à une force totale constante:
- Un objet en chute libre (avec frottements de l’air négligeables), la seule force est alors le poids de l’objet qui reste constant.
- Un projectile lancé (avec frottements de l’air négligeables), lui aussi n’est soumis qu’à son propre poids qui reste constant.
- Un objet qui glisse sans frottement sur une pente d’angle constant (la force de contact du sol et le poids restent constants tout comme la force totale qui en résulte)
- Un corps glissant sans frottement sur une surface plane tracté (ou poussé) grâce à une force constante.
Variation de la vitesse
Comme pour n’importe quel mouvement il existe la relation suivante lorsque le système passe d’une point de sa trajectoire à un point voisin:
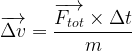
On peut aussi écrire, du point 1 au point 2:
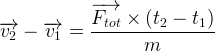
du point point 2 au point 3:
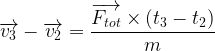
Par conséquent, si l’on ajoute les deux égalités, on obtient:
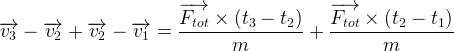
Puisque la force totale est constante il est possible de factoriser le terme où elle intervient:
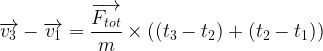
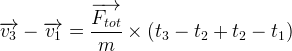
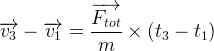
On montre ainsi que l’expression de la variation de vitesse est valable aussi du point 1 au point 3.
En procédant de manière similaire on pourrait montrer que l’expression de la variation de vitesse est valable:
- entre les points 1 et 4
- entre les points 1 et 5
- entre les points 1 et 20
- entre les point 9 et 15
- entre les points 7 et 13
- entres tous les couples de points de la trajectoire !
Plus généralement, lorsque la force totale est constante, la relation entre la variation de vitesse et la force totale est valable entre deux points quelconques de la trajectoire, quel que soit leur éloignement et le temps écoulé.
si au début de son mouvement (t0 = 0 s) le système se trouve au point n°0 et possède une vitesse v0 et si le système atteint le point n° “n” avec une vitesse vn au bout d’un temps tn alors on a la relation suivante
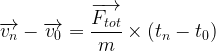
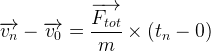
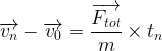
Système immobile au début de son mouvement
Cette situation correspond par exemple à celle d’un corps en chute libre laché sans vitesse initiale.
Dans ce cas la vitesse initiale (v0) est nulle c’est à dire v0 = 0 et la vitesse en un point “n” de la trajectoire est:
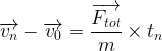
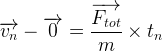
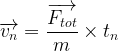
On en déduit donc dans ce cas que:
- le vecteur vitesse a la même direction et le même sens que la force totale
- la vitesse est croissante tout au long du mouvement.
- La vitesse est proportionnelle au temps qui s’est écoulé depuis le début du mouvement.
Cas d’une vitesse initiale ayant même sens et direction que la force totale
Cette situation correspond par exemple à celle corps lancé vers le bas.
L’expression algébrique de la vitesse v au point “n” devient:
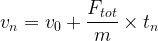
La vitesse est donc croissante au cours du mouvement, elle est une fonction affine du temps écoulé.
Cas d’une vitesse initiale et d’une force totale de même direction et de sens opposés
Cette situation correspond par exemple à celle corps lancé vers verticalement vers le haut.
L’expression algébrique de la vitesse au point “n” devient:
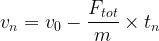
Un tel mouvement se fait trois phases:
- Lors de la première phase la vitesse garde le même sens et la même direction qu’au début de son mouvement mais sa valeur diminue.
- La vitesse finit pas devenir nulle au bout d’un temps
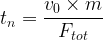
- La vitesse augmente alors et possède la même direction qu’au début de son mouvement mais en pointant dans la direction opposée
A réviser
Cours de seconde:
- Décrire un mouvement
- Système
- Choix un référentiel pour l’étude d’un mouvement
- Trajectoire d’un système
- La vitesse
- Le mouvement
- Modéliser une action sur un système
- Les actions mécaniques
- Les forces
- La force de gravitation
- L’intensité de la pesanteur
- La loi de gravitation universelle
- Le poids, force de pesanteur terrestre
- Principe d’inertie
Les autres cours de première spécialité
- Quantité de matière, masse molaire et concentration
- Réaction d’oxydoréduction et avancement
- Titrage colorimétrique redox
- Schéma de Lewis, géométrie, électronégativité et polarisation
- Cohésion des solides, dissolution, solubilité, hydrophilie et lipophilie
- Structure et nomenclature des espèces organiques
- Synthèses d’espèces organiques
- L’énergie de la matière organique
- Interactions, champs électrostatiques et gravitationnels
- Statique des fluides
Pour approfondir et découvrir
- Addition vectorielle – Article de Wikipedia

Je n’ai pas compris le cas où la force est nulle.