Le principe d'inertie

Principe d’inertie

par

Cours de physique niveau seconde – Mouvement et interaction

Ce cours est aussi disponible en vidéo

Système modélisé par un point

Tout système peut être décrit comme un ensemble de points possédant chacun un Mouvement qui lui est propre.

Chaque point a, en général, un Mouvement qui est proche de celui de ses voisins et au lieu d’étudier chacun d’entre eux en particulier on se contente d’en choisir un seul.

En se limitant à un seul point pour décrire le Mouvement d’un système complet on ne perd qu’une petite partie des informations relatives au Mouvement mais on simplifie ainsi l’étude du Mouvement.

Le Mouvement de tout système peut se limiter à l’étude du Mouvement d’un point particulier de ce système.

Exemples

  • pour décrire le Mouvement d’un ballon le point choisi est en général le centre.
  • pour décrire le Mouvement d’une personne le point en général choisi est le centre de gravité de cette personne
  • Pour décrire le Mouvement d’une voiture on peut choisir un point situé à l’extrémité avant, à l’extrémité arrière ou au centre (mais rarement sur l’une des roues)

Enoncé du principe d’inertie

Le principe d’inertie n’est valable que dans certains référentiels qualifiés de “galiléens”

Enoncé du principe d’inertie:

Si un système est soumis à des forces qui se compensent alors ce système est soit immobile soit en Mouvement rectiligne uniforme.

Remarque

Un Mouvement est rectiligne uniforme si le vecteur vitesse est constant (en norme, direction et sens).

Le principe d’inertie établit un lien entre les forces qui s’exercent sur un système et son Mouvement (ou son absence de Mouvement).

On peut l’utiliser pour démontrer:

Même si l’on n’utilise pas le principe d’inertie on peut exploiter:

  • sa réciproque (qui est vraie aussi)
  • sa contraposée (ce qu’implique la non validation des conditions du principe d’inertie)
  • la réciproque de sa contraposée.

Utilisation du principe d’inertie

Pour utiliser le principe d’inertie on peut suivre la méthode suivante:

  • Puisque le principe d’inertie permet la description d’un Mouvement on commence par choisir un référentiel d’étude.
  • Choisir égalemet le point du système dont on veut étudier le Mouvement.
  • Réaliser un bilan des forces qui s’exercent sur le système
  • Vérifier que les forces qui s’exercent se compensent
  • Conclure en indiquant que le principe d’inertie permet de déduire à l’immobilité ou à un Mouvement rectiligne uniforme.

Réciproque du principe d’inertie

La réciproque du principe d’inertie est aussi vérifiée:

Si un système est immobile ou en Mouvement rectiligne (vecteur vitesse constant) alors les forces qui s’exercent sur le système se compensent.

Par conséquent cette répciproque peut être exploitée pour démontrer que les forces qui s’exercent sur un système se compensent.

La contraposée du principe d’inertie

Si un système est soumis à des forces qui ne se compensent pas alors il n’est ni immobile ni en Mouvement rectiligne uniforme.

Des forces qui ne se compensent pas impliquent une variation du vecteur vitesse c’est à dire que:

  • la valeur de la vitesse varie
  • ou la direction du vecteur vitesse varie ( la trajectoire n’est pas une doite)
  • ou il y a la fois variation de la valeur de la vitesse et de la direction du vecteur vitesse

Réciproque de la contraposée du principe d’inertie

La réciproque de la contraposée du principe d’inertie est aussi vérifiée:

Si un système n’est pas immobile et n’ a pas un Mouvement rectiligne uniforme alors les forces auxquelles qui s’exercent sur le système ne se compensent pas.

Variation du vecteur vitesse d’un système

D’après la contraposée du principe d’inertie si les forces exercées sur un système ne se compensent pas alors son vecteur vitesse varie.

Il est souvent possible d’aller plus loin et de préciser la manière dont varie le vecteur vitesse en fonction des forces.

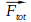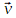Pour cela il faut comparer le vecteur correspondant la somme totale des forces que l’on peut noter Vecteur somme totale des forces au vecteur vitesse vecteur vitesse

D’une manière générale:

  • Si 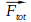Vecteur somme totale des forces a même direction que 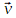vecteur vitesse alors la direction du vecteur vitesse ne varie pas
  • Si 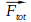Vecteur somme totale des forces a une direction différente de celle de 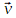vecteur vitesse alors la direction du vecteur vitesse varie et tend à se rapprocher de celle du vecteur force totale.
  • Si 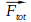Vecteur somme totale des forces a une direction et un sens proche de 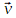vecteur vitessealors la norme du vecteur vitesse augmente
  • Si 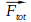Vecteur somme totale des forces a une direction proche de 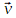vecteur vitesse et un sens opposé alors la norme du vecteur vitesse diminue.

Voir aussi une fiche de cours “Le principe d’inertie“

Les autres cours de physique-chimie niveau seconde