La période

1. Définition, notation et unité
2. Déterminer une période à partir d’un graphe
3. Mesure expérimentale
4. Déterminer la période à partir de la fréquence
5. Quelques valeurs de périodes

Définition, notation et unité

Définition

Lorsqu’un phénomène est périodique sa période correspond à la durée qui sépare deux répétitions successives de ce phénomène.

Remarque: la période est aussi la durée du phénomène lui même.

Notation

La période se note avec la lettre “T” (toujours en majuscule), ce “T” rappelle la nature temporelle de la période et la majuscule la distingue d’un temps ou d’une durée quelconque.

Unité

Puisqu’elle est une durée, on peut exprimer la période à l’aide de n’importe quelle unité de temps (année, mois, jour, heure, minute, seconde, milliseconde etc) mais il est en général préférable d’adopter l’unité la mieux adaptée.

Si la période est destinée à être exploitée dans une relation mathématique (par exemple pour le calcul d’une fréquence) il est probable que cette relation nécessite de l’exprimer en seconde (qui est l’unité du système international) quitte à utiliser une notation scientifique.

Déterminer une période à partir d’un graphe

Lorsqu’un graphe représente les variations d’une grandeur X (qui peut être une tension, une cordonnée, une longueur, un angle, une température etc…) en fonction du temps alors il est possible d’exploiter ce graphe pour déterminer la période T en suivant la méthode suivante:

  

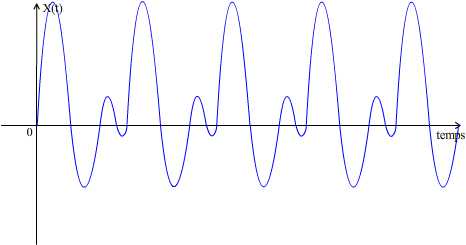
• Repérer sur le graphe le motif élémentaire, c’est à dire la plus petite portion qui se répète tout au long de la courbe. Il est en réalité possible de repérer de nombreux motifs différents (qui coïncident tous avec la même période) mais en pratique il est préférable de retenir celui dont les limites sont facilement repérable (celles qui par exemple sont située sur l’axe des abscisses ou qui coïncident avec un maximum ou un minimum)

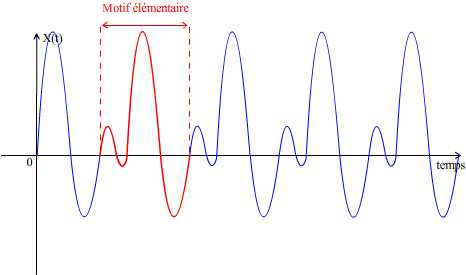
• Déterminer la coordonnée temporelle t1 associé à l’abscisse du premier point du motif puis la coordonnée temporelle t2 correspondant à l’abscisse de son dernier point.

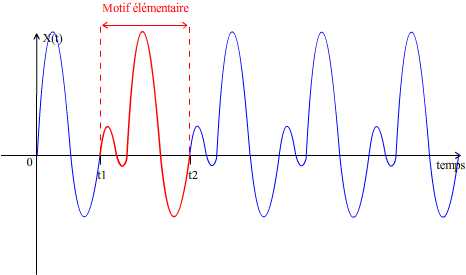
• La période T correspond à la différente entre t2 et t1: T = t2 – t1

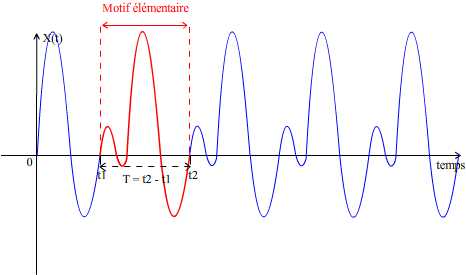
Il est possible de déterminer la période avec une meilleure précision en ne considérant plus un seul motif mais une succession de 2, 3, 4 5, 10 motifs ou plus. Dans ce cas:

• t1 est toujours l’abscisse du premier point du premier motif
• t2 est l’abscisse du dernier point du n^ième motif
• La période T est obtenue en divisant la différence des deux temps précédent par le nombre “n” de motifs utilisés: T = (t2 – t1)/n

Mesure expérimentale

Dans le cas la plus simple, si les variations périodiques peuvent être observées directement (oscillations d’un pendule simple, mouvement de va et vient d’un objet suspendu à un ressort etc) et si la valeur de la période est supérieure à une seconde alors sa mesure peut se faire par simple chronométrage, il suffit:

• de choisir une configuration facilement repérable (une disposition particulière du système que l’on peut prendre comme point de repère)
• de chronométrer le temps qui s’écoule entre deux passages successifs par cette configuration (ce temps correspond à la période)

Comme toute mesure, le chronométrage est entachée d’une certaine incertitude (une marge d’erreur) qui résulte, entre autres, du temps de réaction pour déclencher le chronomètre et de la difficulté à distinguer le repère choisi, il est cependant possible de diminuer cette incertitude en ne mesurant pas une période mais un nombre “n” (4, 8, 10 20 etc) de périodes . La période est obtenue en divisant la durée totale des “n” répétitions du phénomène par le nombre “n” mais l’incertitude est aussi divisée du même facteur.

Si la grandeur variant périodiquement n’est pas accessible directement car il s’agit d’un mouvement trop rapide ou d’une grandeur physique telle que la tension électrique, la température, l’intensité lumineuse etc alors il est nécessaire défaire appelles à un système d’enregistrement: vidéo, capteurs, interface, sonde etc qui permette soit de visualiser le phénomène soit de le traduire en signaux électriques exploitables.

Déterminer la période à partir de la fréquence

La période d’un phénomène (ou d’un signal) périodique correspond à l’inverse de sa fréquence (f) par conséquent elle peut être calculée en utilisant la relation

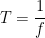
où:

• f est la fréquence en hertz (Hz)
• T est la période en seconde (s)

Exemple de calcul de période à partir d’une fréquence:

• si la fréquence est de 20 hertz alors T = 1 / 20 = 0,050 s
• si la fréquence est de 0,0100 hertz alors T = 1: 0,0100 = 100 s
• si la fréquence est de 10 kHz alors f = 10 000 Hz et T = 1/10 000 = 0,00010 s

Quelques valeurs de périodes

Phénomène	Période
Note do octave 0	31 ms
Note Si octave 0	16 ms
Rotation terrestre	23 h 56 min
Révolution terrestre	365,24 jour
Courant alternatif du secteur	20 ms
Elections présidentielles françaises	5 ans