- Qu’est-ce que la gravitation ?
- Le point d’application de la force de gravitation
- La direction de la force de gravitation
- Le sens de la force de gravitation
- La valeur de la force de gravitation
- Effets de la force de gravitation
- Représentation vectorielle
Qu’est-ce que la gravitation ?
L’interaction gravitationnelle s’exerce entre tous les systèmes possédant une masse (autant dire, à quelques rares exceptions comme le photon et peut-être les neutrinos , presque tous les systèmes) sans limite de distance. Elle est toujours attractive (contrairement aux forces électriques et magnétiques qui peuvent aussi être répulsives) c’est à dire qu’elle attire le système soumis à cette force vers celui qui l’exerce.
Le point d’application de la force de gravitation
La force de gravitation est une force répartie en volume, c’est à dire que chaque particule du système subit cette force mais on peut considérer que la résultante s’applique en point particulier appelé centre de gravité (noté G), ce point est en général confondu avec un autre point appelé centre d’inertie qui correspond au barycentre des masses du système, soit le point “le plus central de la répartition de masse”. Pour un système homogène ou pour un système à symétrie centrale alors il correspond simplement au centre géométrique.
En résumé le point d’application de la force de gravitation est le centre de gravité noté G, qui correspond le plus souvent au centre d’inertie et au centre géométrique du système.
La direction de la force de gravitation
Il s’agit de la droite joignant les centres de gravité des deux systèmes en interaction
Le sens de la force de gravitation
La force de gravitation exercée par un système A sur un système B est orienté du centre de gravité de B vers le centre de gravité de A
La valeur de la force de gravitation
Valeur de la force de gravitation exercée par un corps A sur un corps B est donnée par la loi de gravitation universelle qui peut s’exprimer par la relation suivante:
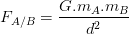
où:
- mA est la masse du corps A en kilogramme (kg)
- mB est la masse du corps B en kilogramme (kg)
- d est la distance entre le centre de gravité du corps A et celui du corps B
- G est la constante de gravitation universelle avec G = 6,67. 10-11 USI USI (unité du système international)
- FA/B est la valeur de la forces de gravitation exercée par le système A sur le système B en newton (N)
Cette force est aussi celle exercée par le corps B sur le corps ainsi on a: 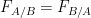
Effets de la force de gravitation
Cette force s’exerce entre tous les corps possédant une masse mais sa valeur est en général trop faible pour que ses effets soient remarquables lorsque les deux systèmes ont masse insuffisante : particules subatomiques, atomes, molécules, objets à l’échelle humaine etc.
Les effets de la gravitation ne deviennent non négligeables que lorsqu’au moins l’un des deux systèmes en interaction est un astre: entre la Terre et une personne, en la Lune et la Terre etc.
Lorsque la gravitation s’exerce entre un astre et un corps de masse réduite alors elle est assimilée à ce que l’on appelle le “poids” de ce corps. Elle le maintient à sa surface et provoque sa chute lorsqu’il s’en éloigne.
Lorsque la gravitation s’exerce entre deux astres elle peut, suivant les conditions, soit provoquer leur collision ou permettre à l’astre de masse la plus petite d’adopter une orbite autour de l’astre le plus massique (ce dernier cas est possible si le “petit astre possède un mouvement adapté)
Représentation vectorielle
Si l’on souhaite représenter par des vecteurs les forces de gravitation s’exerçant entre deux corps A et B alors chaque vecteur:
- a son origine au centre du système
- a même direction que l’axe passant par les deux centres de gravité
- est orienté vers l’autre système.
Les deux vecteurs ont:
- même direction
- même longueur
- des sens opposés
en résumé: 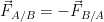
Exemple
Interaction gravitationnelle entre la Terre et la Lune

