Cours de physique-chimie | première spécialité
Ce cours correspond à la partie “Aspects énergétiques des phénomènes mécaniques” du programme de première spécialité.
Il est situé dans la partie du programme “L’énergie : conversions et transferts”
- L’énergie cinétique
- Travail d’une force
- Forces conservatives et non conservatives
- Théorème de l’énergie cinétique
- Energie potentielle
- Energie mécanique
REVISER – AUTRES COURS DE PREMIERE SPECIALITE – APPROFONDIR ET DECOUVRIR
L’énergie cinétique
L’énergie cinétique est l’énergie du mouvement
Si un système de masse “m” se déplace à une vitesse “v” dans un référentiel donné alors dans ce référentiel l’énergie cinétique du système se calcule grâce à la relation suivante:
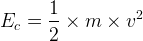
où:
- Ec est l’énergie cinétique du système en Joule (J)
- m est la masse du système en kilogramme (kg)
- v est la vitesse du système en mètre par seconde (m.s-1)
VOIR AUSSI FICHE DE COURS L’énergie cinétique
Travail d’une force
Définition du travail
Lorsqu’un système en mouvement se déplace d’un point A vers un point B tout en étant soumis à une force 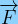 alors la variation d’énergie du système, sous l’influence de cette force, est appelé travail.
alors la variation d’énergie du système, sous l’influence de cette force, est appelé travail.
Le travail d’une force  sur un système se déplaçant d’un point A à un point B est noté:
sur un système se déplaçant d’un point A à un point B est noté:
WAB( )
)
Remarque: “W” comme “Work” qui signifie “travail” en anglais.
L’unité du travail est la même que celle de l’énergie: le Joule (J)
Travail d’une force constante
Si un système se déplaçant d’un point A à un point B est soumis à une force  constante (elle garde la même direction, le même sens et la même valeur) alors le travail WAB(
constante (elle garde la même direction, le même sens et la même valeur) alors le travail WAB( ) de cette force correspond au produit scalaire de ce vecteur force
) de cette force correspond au produit scalaire de ce vecteur force  par le vecteur déplacement
par le vecteur déplacement 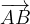 .
.
Le travail peut alors s’exprimer par la relation:
WAB(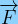 ) =
) = 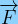 .
.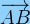
Si l’angle entre 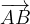 et
et  est “α” alors le travail peut se calculer grâce la formule suivante (qui dérive des propriétés du produit scalaire):
est “α” alors le travail peut se calculer grâce la formule suivante (qui dérive des propriétés du produit scalaire):
WAB(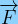 ) = F x AB x cos (α)
) = F x AB x cos (α)
où
- F est la valeur de la force en Newton (N)
- AB est la distance entre le premier point et le dernier point du mouvement
- α est l’angle entre le vecteur force
 et le vecteur déplacement
et le vecteur déplacement 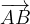 en degré
en degré
Différents cas possibles:
- Si α < 90 ° (angle aigu entre les deux vecteurs) alors cos (α) > 0 et WAB(
 ) > 0 on dit que le travail est moteur car le système reçoit de l’énergie sous l’influence de la force.
) > 0 on dit que le travail est moteur car le système reçoit de l’énergie sous l’influence de la force. - Si α > 90 ° (angle obtus entre les deux vecteurs) alors cos (α) < 0 et WAB(
 ) < 0 on dit que le travail est résistant car le système perd de l’énergie sous l’influence de la force.
) < 0 on dit que le travail est résistant car le système perd de l’énergie sous l’influence de la force. - Si α = 90 ° (Force perpendiculaire au mouvement) alors cos (α) = 0 et WAB(
 ) = 0 on dit que la force ne travail pas car elle n’a pas d’influence sur l’énergie du système.
) = 0 on dit que la force ne travail pas car elle n’a pas d’influence sur l’énergie du système.
Remarque
D’une manière générale le travail d’une force qui reste en permanence perpendiculaire au déplacement est nul.
Travail du poids
Le poids peut être considéré comme une force constante lors d’un mouvement de faible amplitude dans le champ de pesanteur terrestre, par conséquent on l’exprimer par la relation:
WAB(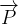 ) =P x AB x cos (α)
) =P x AB x cos (α)
Le terme AB x cos (α) correspond à la projection du segment AB sur l’axe horizontal et l’on a donc l’égalité AB x cos (α) = yA – yB
Le travail du poids d’un système lors du mouvement d’un point A à un point B est donc:
WAB(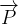 ) =P x (yA – yB)
) =P x (yA – yB)
Puisque le poids P est donné par la relation P = m x g on obtient donc:
WAB(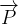 ) =m x gx (yA – yB)
) =m x gx (yA – yB)
où:
- WAB(
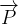 ) est le travail du poids lors du mouvement de A à B en Joule (J)
) est le travail du poids lors du mouvement de A à B en Joule (J) - m est la masse du système en kilogramme (kg)
- g est l’intensité de la pesanteur ( g = 9,81 N.kg-1)
- yA est l’altitude du point A en mètre (m)
- yB est l’altitude du point B en mètre (m)
Travail des forces de frottement
Les forces de frottement peuvent s’exercer lorsque le mouvement d’un système se fait dans un fluide (air, eau etc) ou au contact d’une surface: elles s’opposent toujours au mouvement.
Dans le cas d’un système animé d’un mouvement rectiligne soumis à une force de frottement “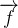 ” constante alors
” constante alors 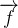 et le vecteur déplacement
et le vecteur déplacement 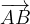 ont des sens opposés, l’angle entre ces deux vecteurs est donc de 180°
ont des sens opposés, l’angle entre ces deux vecteurs est donc de 180°
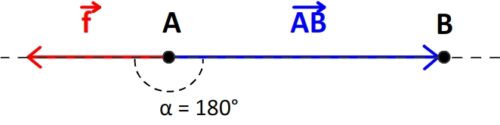
L’expression du travail de la force de frottement “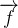 ” devient donc:
” devient donc:
WAB(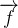 ) = f x AB x cos (α)
) = f x AB x cos (α)
WAB(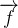 ) = f x AB x cos (180)
) = f x AB x cos (180)
WAB(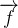 ) = f x AB x (-1)
) = f x AB x (-1)
WAB(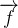 ) = – f x AB
) = – f x AB
Expression du travail d’une force de frottement: WAB(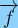 ) = – f x AB
) = – f x AB
Forces conservatives et non conservatives
Les forces sont classées en deux catégories:
- Une force est dite conservative si son travail ne dépend pas du chemin suivi.
D’un point A à un point B le travail WAB( ) d’une force conservative possède la même valeur quelle que soit la trajectoire suivie entre A et B.
) d’une force conservative possède la même valeur quelle que soit la trajectoire suivie entre A et B.
Exemple de force conservative: le poids
- Une force est dite non conservative si son travail dépend du chemin suivi.
D’un point A à un point B le travail WAB( ) d’une force non conservative prend des valeurs différentes pour des trajectoires différentes.
) d’une force non conservative prend des valeurs différentes pour des trajectoires différentes.
Exemple de force non conservative: les forces de frottement.
Théorème de l’énergie cinétique
Enoncé du théorème de l’énergie cinétique:
Si un corps est en mouvement d’un point A à un point B alors la variation de son énergie cinétique correspond à la somme des travaux de toutes les forces qui s’exercent sur lui pendant ce mouvement.
Le théorème de l’énergie cinétique peut se traduire par la relation:
ΔEc = Σ WAB( )
)
ou :
Ec(B) – Ec(A) = Σ WAB( )
)
ou encore:
(½).m.vB2 – (½).m.vA2 = Σ WAB( )
)
Dans le cas où le système n’est soumis qu’à une seule force 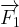 :
:
Ec(B) – Ec(A) = WAB(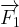 )
)
Dans le cas où le système est soumis à deux forces ( 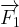 et
et 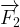 ) :
) :
Ec(B) – Ec(A) = WAB(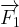 ) + WAB(
) + WAB(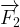 )
)
Dans le cas où le système est soumis à trois forces ( 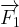 ,
, 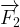 et
et 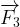 ) :
) :
Ec(B) – Ec(A) = WAB(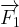 ) + WAB(
) + WAB(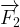 ) +WAB(
) +WAB(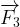 )
)
etc
Le théorème de l’énergie cinétique peut être exploité:
- pour déterminer la vitesse du système en un point donné de sa trajectoire
- pour déterminer la valeur d’une force constante exercée sur un système lorsque la vitesse au cours du mouvement est connue
- pour déterminer la masse d’un système en mouvement.
Energie potentielle
Définition
Tout force conservative  est associée à une énergie potentielle notée Ep.
est associée à une énergie potentielle notée Ep.
Cette énergie potentielle est caractérisée par une variation qui est l’opposée du travail des forces, par conséquent:
ΔEp = – WAB(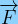 )
)
ou encore:
Ep(B) – Ep(A) = – WAB(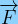 )
)
Ce qui est équivalent à la relation suivante:
Ep(A) – Ep(B) = WAB(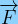 )
)
Energie potentielle de pesanteur
Le poids est une force conservative, on lui associe donc une énergie potentielle dite “énergie potentielle de pesanteur”.
Elle se not Epp et s’exprime par la formule:
Ep(A) = m.g.yA + constante
où:
- Ep(A) est l’énergie du système situé en un point “A” en joule (J)
- “m” est la masse du système en kilogramme (kg)
- “g” est l’intensité de la pesanteur (g = 9,81 N.kg-1)
- yA est l’altitude du point A en mètre (m)
- la constante est une grandeur qui dépend de l’origine choisie pour exprimer l’altitude
La variation d’énergie potentielle de pesanteur entre le point A et le point B est donc:
Ep(B) – Ep(A) = ( m.g.yB + constante) – (m.g.yA + constante)
Ep(B) – Ep(A) = m.g.yB + constante – m.g.yA – constante
Ep(B) – Ep(A) = m.g.yB – m.g.yA + constante – constante
Ep(B) – Ep(A) = m.g.(yB – yA) + 0
Ep(B) – Ep(A) = m.g.(yB – yA)
VOIR AUSSI FICHE DE COURS: L’énergie potentielle de pesanteur
Energie mécanique
Définition
L’énergie mécanique d’un système est définie comme la somme de son énergie cinétique et de son énergie potentielle de pesanteur.
Elle se note Em et s’exprime en Joule (J)
Elle peut être exprimée par la relation:
Em = Ec + Ep
où:
- Em est l’énergie mécanique du système en Joule (J)
- Ec est l’énergie cinétique du système en Joule (J)
- Epp est l’énergie potentielle du système en Joule (J)
On peut également exprimer la variation d’énergie mécanique ΔEm à partir des variations d’énergie cinétique ΔEc et d’énergie potentielle de pesanteur ΔEpp :
ΔEm = ΔEc + ΔEpp
VOIR FICHE DE COURS: L’énergie mécanique
Théorème de l’énergie mécanique
Enoncé du theorème de l’énergie mécanique:
La variation d’énergie mécanique d’un système correspond à la somme des travaux des forces non conservatives exercées sur ce système.
Ce théorème peut se traduire par la relation suivante:
ΔEm = ΣWAB(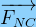 )
)
où la variation d’énergie mécanique ainsi que la somme des travaux des forces non conservatives sont exprimées en Joule.
Non conservation de l’énergie mécanique
D’après le théorème de l’énergie mécanique si le système est soumis à des forces non conservatives alors l’énergie mécanique varie, elle ne se conserve pas.
Si le travail des forces non conservatives est moteur ( WAB(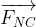 ) > 0 ) alors la variation d’énergie mécanique est positive ( ΔEm > 0 ) donc l’énergie mécanique augmente.
) > 0 ) alors la variation d’énergie mécanique est positive ( ΔEm > 0 ) donc l’énergie mécanique augmente.
Si le travail des forces non conservatives est résistant ( WAB(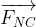 ) < 0 ) alors la variation d’énergie mécanique est négative ( ΔEm > 0 ) donc l’énergie mécanique diminue
) < 0 ) alors la variation d’énergie mécanique est négative ( ΔEm > 0 ) donc l’énergie mécanique diminue
Conservation de l’énergie mécanique
Si le système n’est soumis qu’à des forces conservatives alors WAB(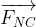 ) = 0 par conséquent, d’après le théorème de l’énergie mécanique:
) = 0 par conséquent, d’après le théorème de l’énergie mécanique:
ΔEm = Σ WAB(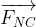 )
)
ΔEm = 0
La variation d’énergie cinétique est nulle ce qui signifie qu’elle reste constante.
Lorsqu’un système n’est soumis qu’à des forces conservatives alors énergie mécanique se conserve:
Em = constante
Em(A) = Em(B)
Etant donné que l’énergie mécanique d’un système correspond à la somme de son énergie cinétique et de son énergie potentielle de pesanteur alors la conservation de l’énergie mécanique implique que la variation de l’une est compensée par une variation opposée de l’autre:
ΔEc = – ΔEpp
En cas de de conservation de l’énergie mécanique:
- Lorsque l’énergie cinétique diminue alors l’énergie potentielle de pesanteur augmente.
- Lorsque l’énergie cinétique augmente alors l’énergie potentielle de pesanteur diminue.
- Lorsque l’énergie potentielle de pesanteur diminue alors l’énergie cinétique augmente.
- Lorsque l’énergie potentielle de pesanteur augmente alors l’énergie cinétique diminue.
A réviser
Cours de seconde:
- Décrire un mouvement
- Système
- Choix un référentiel pour l’étude d’un mouvement
- Trajectoire d’un système
- La vitesse
- Le mouvement
- Modéliser une action sur un système
- Les actions mécaniques
- Les forces
- La force de gravitation
- L’intensité de la pesanteur
- La loi de gravitation universelle
- Le poids, force de pesanteur terrestre
Les autres cours de première spécialité
- Quantité de matière, masse molaire et concentration
- Réaction d’oxydoréduction et avancement
- Titrage colorimétrique redox
- Schéma de Lewis, géométrie, électronégativité et polarisation
- Cohésion des solides, dissolution, solubilité, hydrophilie et lipophilie
- Structure et nomenclature des espèces organiques
- Synthèses d’espèces organiques
- L’énergie de la matière organique
- Interactions, champs électrostatiques et gravitationnels
- Statique des fluides
- Variations de vecteur vitesse
- Courant électrique et bilans énergétiques
Pour approfondir et découvrir
- L’énergie cinétique – C’est pas sorcier (Youtube)
