Cours de physique – niveau classe de première spécialité
- Notation et unité
- Définition du champ de gravitation
- Lignes du champ de gravitation
- Expression du champ de gravitation
- Force exercée sur un corps situé dans un champ de gravitation
- Champ de gravitation et champ de pesanteur
Notation et unité
Le champ de gravitation se note G majuscule mais afin d’éviter toute confusion avec la constante de gravitation universelle on utilise la notation calligraphiée mais sur cette page il sera simplement noté Gchamp.
Sont unité est le Newton par kilogramme (N/kg) qui est équivalente au mètre par seconde au carré (m.s-2), soit la même unité qu’une accélération.
Définition du champ de gravitation
Il s’agit d’un champ traduisant l’influence gravitationnelle d’un corps doté d’une masse sur l’espace qui l’entoure.
Le champ de gravitation que produit en un point de l’espace A’ une masse ponctuelle m située un point A:
- a même direction et même sens que la force gravitationnelle qu’exercerait cette masse sur une masse ponctuelle m’ située en A’.
- a pour valeur Gchamp = F/m’
Où m’ serait une masse ponctuelle située en A’ et F la force de gravitation exercée par le corps de masse m sur celui de masse m’
Lignes du champ de gravitation
Elles sont orientées vers le centre de gravité du corps produisant le champ. Dans le cas d’un corps à symétrie sphérique (comme par exemple une planète), les lignes de champ passent par le centre de la sphère.
Exemple
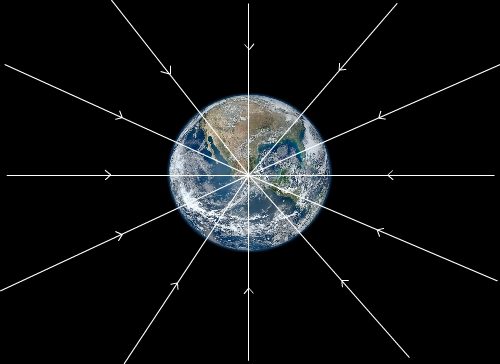
Expression du champ de gravitation
Dans le cas d’un corps ponctuel de masse m celui-ci exerce sur tout corps ponctuel de masse m’ une force dont l’expression est donnée par la loi de gravitation universelle :
F = G.m.m.’/d2
Où d correspond à la distance entre les deux corps.
Cette expression peut être généralisée aux corps non ponctuels, dans ce cas “d” représente la distance entre les centres de gravité des deux corps.
Puisque la valeur du champ est donné par la relation Gchamp = F/m’ on obtient donc l’expression suivante:
Gchamp = G.m/d2
Force exercée sur un corps situé dans un champ de gravitation
La relation définissant le champ de gravitation permet aussi d’exprimer la valeur de la force gravitationnelle exercée sur tout corps soumis à ce champ.
Si un corps de masse m est soumis à un champ gravitationnel Gchamp alors il s’exerce sur ce dernier une force:
- ayant même direction et même sens que le champ de gravitation
- de valeur F = m.Gchamp
Champ de gravitation et champ de pesanteur
Le champ de pesanteur est un cas particulier de champ de gravitation, ces champs sont assimilables l’un à l’autre lorsque la force de gravitation est assimilable au poids c’est à dire:
- pour un espace proche de la surface d’un astre
- lorsque cet espace à une étendue limitée ( de faibles dimensions par rapport à la circonférence de l’astre)
- lorsque ce espace à une hauteur négligeable devant le rayon de l’astre (quelques centaines de mètres voire quelques kilomètres pour la Terre)
- lorsque la force de gravitation (assimilable au poids) s’exprime par la relation P=m.g.
C’est un champ qui peut être considéré comme uniforme, il est toujours :
- vertical
- orienté vers le bas
- de valeur égale à l’intensité de la pesanteur g (9,81 N/kg à la surface de la Terre)
Il est défini comme le rapport du poids P d’un système par la masse de ce système soit:
P/m = m.g/m
= g
Notions de seconde à réviser
- Les actions mécaniques
- Les forces
- La force de gravitation
- L’intensité de la pesanteur
- La loi de gravitation universelle
- Le poids, force de pesanteur terrestre
